Visualizing Overlapping Biclusterings and Boolean Matrix Factorizations

Finding (bi-)clusters in bipartite graphs is a popular data analysis approach. Analysts typically want to visualize the clusters, which is simple as long as the clusters are disjoint. However, many modern algorithms find overlapping clusters, making visualization more complicated. In this paper, we study the problem of visualizing \emph{a given clustering} of overlapping clusters in bipartite graphs and the related problem of visualizing Boolean Matrix Factorizations. We conceptualize three different objectives that any good visualization should satisfy: (1) proximity of cluster elements, (2) large consecutive areas of elements from the same cluster, and (3) large uninterrupted areas in the visualization, regardless of the cluster membership. We provide objective functions that capture these goals and algorithms that optimize these objective functions. Interestingly, in experiments on real-world datasets, we find that the best trade-off between these competing goals is achieved by a novel heuristic, which locally aims to place rows and columns with similar cluster membership next to each other.

Adversaries with Limited Information in the Friedkin--Johnsen Model

In recent years, online social networks have been the target of adversaries who seek to introduce discord into societies, to undermine democracies and to destabilize communities. Often the goal is not to favor a certain side of a conflict but to increase disagreement and polarization. To get a mathematical understanding of such attacks, researchers use opinion-formation models from sociology, such as the Friedkin--Johnsen model, and formally study how much discord the adversary can produce when altering the opinions for only a small set of users. In this line of work, it is commonly assumed that the adversary has full knowledge about the network topology and the opinions of all users. However, the latter assumption is often unrealistic in practice, where user opinions are not available or simply difficult to estimate accurately. To address this concern, we raise the following question: Can an attacker sow discord in a social network, even when only the network topology is known? We answer this question affirmatively. We present approximation algorithms for detecting a small set of users who are highly influential for the disagreement and polarization in the network. We show that when the adversary radicalizes these users and if the initial disagreement/polarization in the network is not very high, then our method gives a constant-factor approximation on the setting when the user opinions are known. To find the set of influential users, we provide a novel approximation algorithm for a variant of MaxCut in graphs with positive and negative edge weights. We experimentally evaluate our methods, which have access only to the network topology, and we find that they have similar performance as methods that have access to the network topology and all user opinions. We further present an NP-hardness proof, which was an open question by Chen and Racz [IEEE Trans. Netw. Sci. Eng., 2021].

Sublinear-Time Clustering Oracle for Signed Graphs

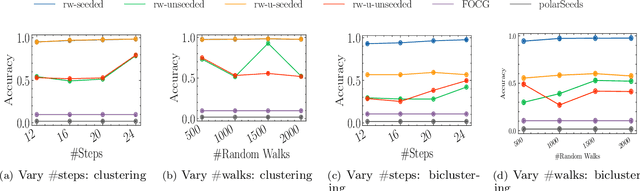
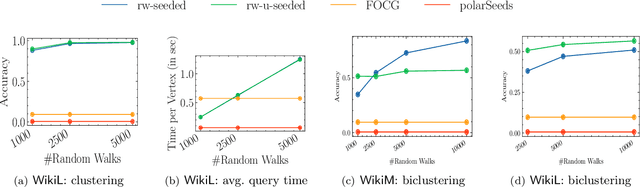
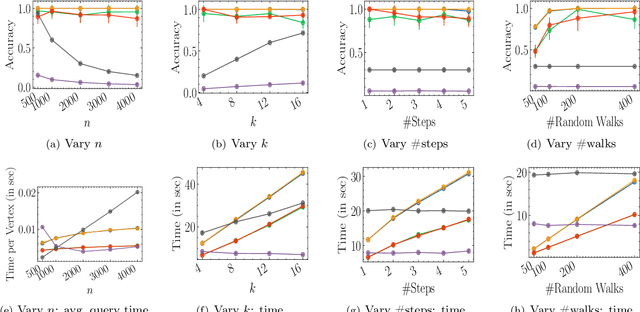
Social networks are often modeled using signed graphs, where vertices correspond to users and edges have a sign that indicates whether an interaction between users was positive or negative. The arising signed graphs typically contain a clear community structure in the sense that the graph can be partitioned into a small number of polarized communities, each defining a sparse cut and indivisible into smaller polarized sub-communities. We provide a local clustering oracle for signed graphs with such a clear community structure, that can answer membership queries, i.e., "Given a vertex $v$, which community does $v$ belong to?", in sublinear time by reading only a small portion of the graph. Formally, when the graph has bounded maximum degree and the number of communities is at most $O(\log n)$, then with $\tilde{O}(\sqrt{n}\operatorname{poly}(1/\varepsilon))$ preprocessing time, our oracle can answer each membership query in $\tilde{O}(\sqrt{n}\operatorname{poly}(1/\varepsilon))$ time, and it correctly classifies a $(1-\varepsilon)$-fraction of vertices w.r.t. a set of hidden planted ground-truth communities. Our oracle is desirable in applications where the clustering information is needed for only a small number of vertices. Previously, such local clustering oracles were only known for unsigned graphs; our generalization to signed graphs requires a number of new ideas and gives a novel spectral analysis of the behavior of random walks with signs. We evaluate our algorithm for constructing such an oracle and answering membership queries on both synthetic and real-world datasets, validating its performance in practice.

Biclustering and Boolean Matrix Factorization in Data Streams

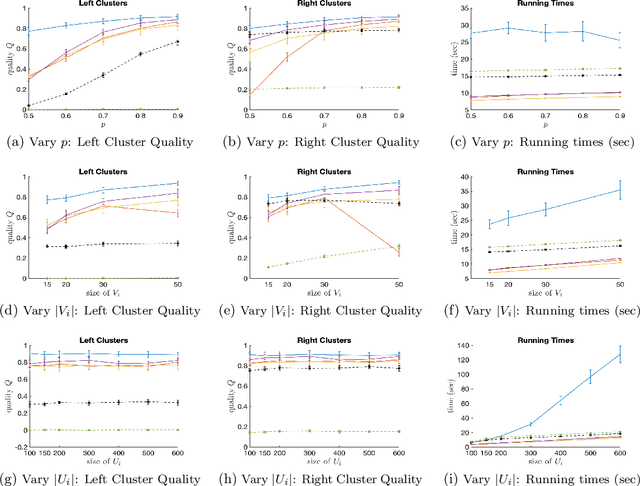
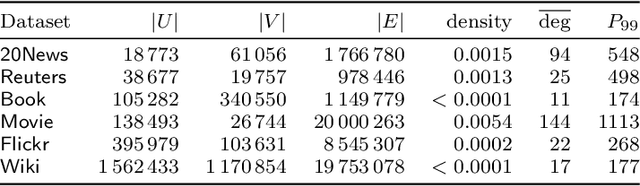
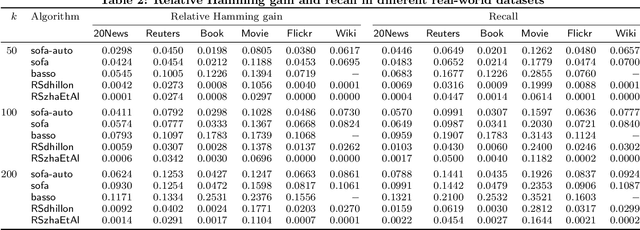
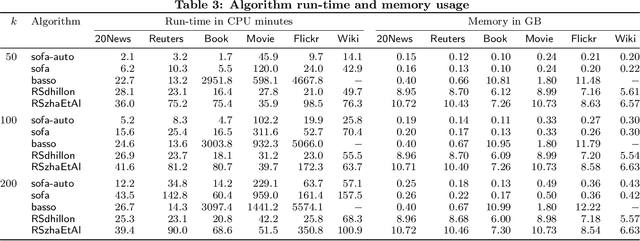
We study the clustering of bipartite graphs and Boolean matrix factorization in data streams. We consider a streaming setting in which the vertices from the left side of the graph arrive one by one together with all of their incident edges. We provide an algorithm that, after one pass over the stream, recovers the set of clusters on the right side of the graph using sublinear space; to the best of our knowledge, this is the first algorithm with this property. We also show that after a second pass over the stream, the left clusters of the bipartite graph can be recovered and we show how to extend our algorithm to solve the Boolean matrix factorization problem (by exploiting the correspondence of Boolean matrices and bipartite graphs). We evaluate an implementation of the algorithm on synthetic data and on real-world data. On real-world datasets the algorithm is orders of magnitudes faster than a static baseline algorithm while providing quality results within a factor 2 of the baseline algorithm. Our algorithm scales linearly in the number of edges in the graph. Finally, we analyze the algorithm theoretically and provide sufficient conditions under which the algorithm recovers a set of planted clusters under a standard random graph model.

Recent Developments in Boolean Matrix Factorization

The goal of Boolean Matrix Factorization (BMF) is to approximate a given binary matrix as the product of two low-rank binary factor matrices, where the product of the factor matrices is computed under the Boolean algebra. While the problem is computationally hard, it is also attractive because the binary nature of the factor matrices makes them highly interpretable. In the last decade, BMF has received a considerable amount of attention in the data mining and formal concept analysis communities and, more recently, the machine learning and the theory communities also started studying BMF. In this survey, we give a concise summary of the efforts of all of these communities and raise some open questions which in our opinion require further investigation.