On multipolar magnetic anomaly detection: multipolar signal subspaces, an analytical orthonormal basis, multipolar truncature and detection performance

In this paper, we consider the magnetic anomaly detection problem which aims to find hidden ferromagnetic masses by estimating the weak perturbation they induce on local Earth's magnetic field. We consider classical detection schemes that rely on signals recorded on a moving sensor, and modeling of the source as a function of unknown parameters. As the usual spherical harmonic decomposition of the anomaly has to be truncated in practice, we study the signal vector subspaces induced by each multipole of the decomposition, proving they are not in direct sum, and discussing the impact it has on the choice of the truncation order. Further, to ease the detection strategy based on generalized likelihood ratio test, we rely on orthogonal polynomials theory to derive an analytical set of orthonormal functions (multipolar orthonormal basis functions) that spans the space of the noise-free measured signal. Finally, based on the subspace structure of the multipole vector spaces, we study the impact of the truncation order on the detection performance, beyond the issue of potential surparametrization, and the behaviour of the information criteria used to choose this order.

Random matrix-improved estimation of covariance matrix distances

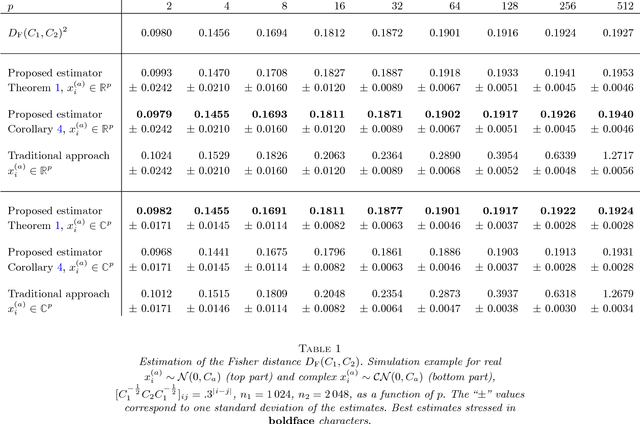
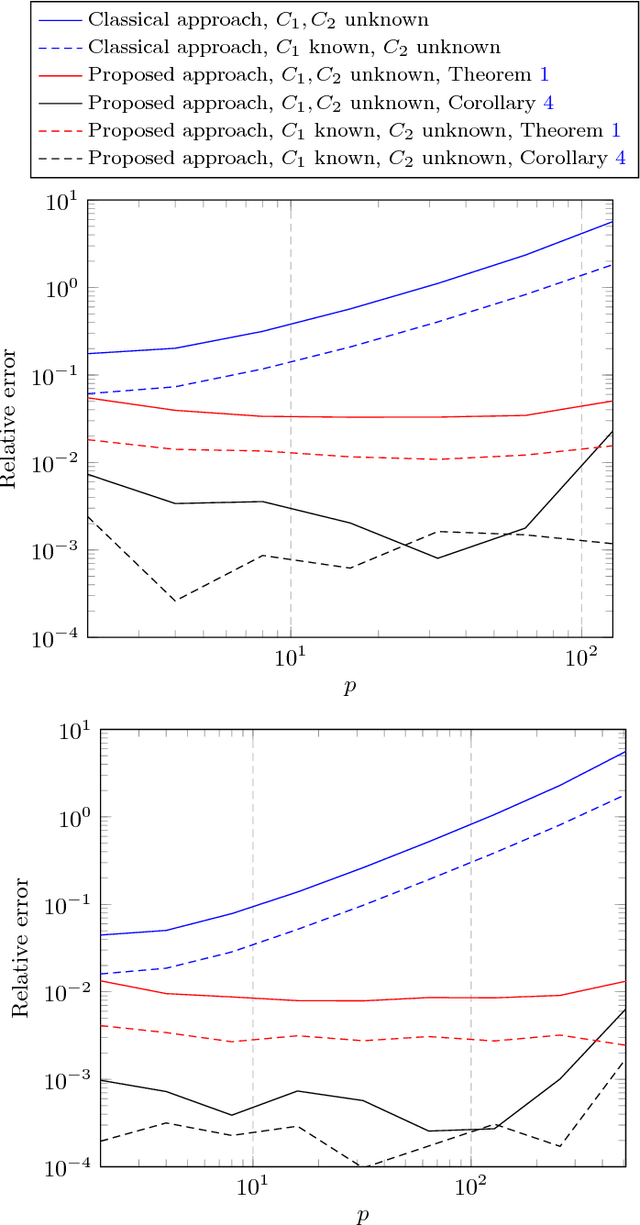
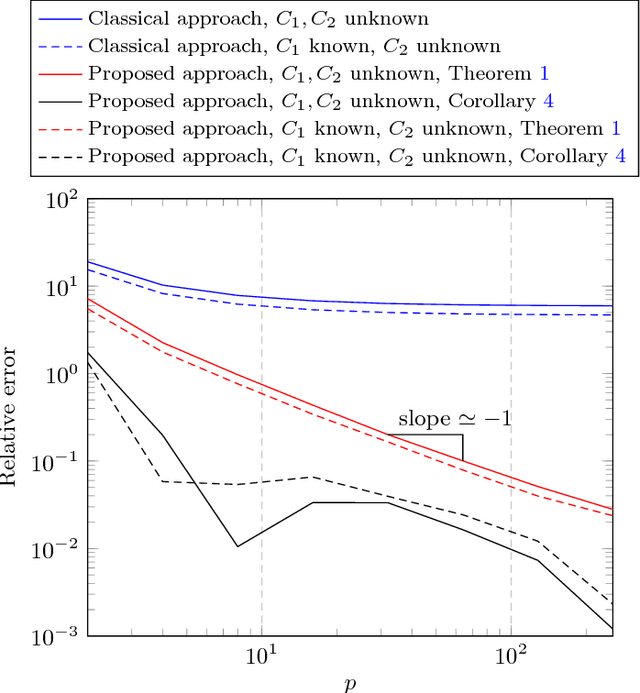
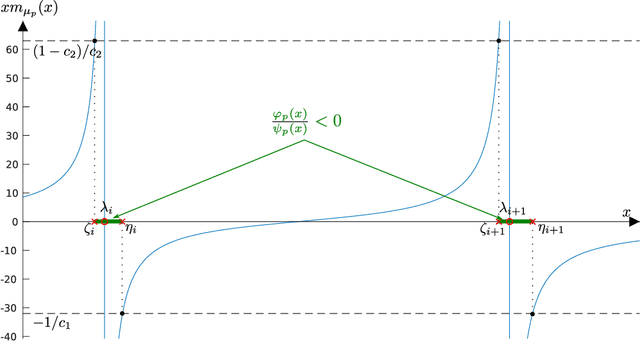
Given two sets $x_1^{(1)},\ldots,x_{n_1}^{(1)}$ and $x_1^{(2)},\ldots,x_{n_2}^{(2)}\in\mathbb{R}^p$ (or $\mathbb{C}^p$) of random vectors with zero mean and positive definite covariance matrices $C_1$ and $C_2\in\mathbb{R}^{p\times p}$ (or $\mathbb{C}^{p\times p}$), respectively, this article provides novel estimators for a wide range of distances between $C_1$ and $C_2$ (along with divergences between some zero mean and covariance $C_1$ or $C_2$ probability measures) of the form $\frac1p\sum_{i=1}^n f(\lambda_i(C_1^{-1}C_2))$ (with $\lambda_i(X)$ the eigenvalues of matrix $X$). These estimators are derived using recent advances in the field of random matrix theory and are asymptotically consistent as $n_1,n_2,p\to\infty$ with non trivial ratios $p/n_1<1$ and $p/n_2<1$ (the case $p/n_2>1$ is also discussed). A first "generic" estimator, valid for a large set of $f$ functions, is provided under the form of a complex integral. Then, for a selected set of $f$'s of practical interest (namely, $f(t)=t$, $f(t)=\log(t)$, $f(t)=\log(1+st)$ and $f(t)=\log^2(t)$), a closed-form expression is provided. Beside theoretical findings, simulation results suggest an outstanding performance advantage for the proposed estimators when compared to the classical "plug-in" estimator $\frac1p\sum_{i=1}^n f(\lambda_i(\hat C_1^{-1}\hat C_2))$ (with $\hat C_a=\frac1{n_a}\sum_{i=1}^{n_a}x_i^{(a)}x_i^{(a){\sf T}}$), and this even for very small values of $n_1,n_2,p$.