Random matrix-improved estimation of covariance matrix distances
Paper and Code
Oct 10, 2018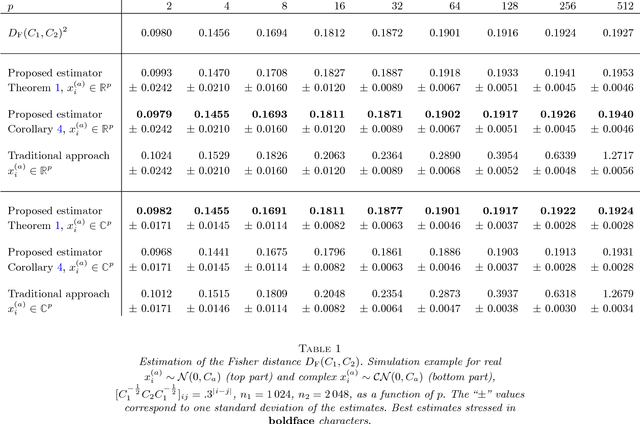
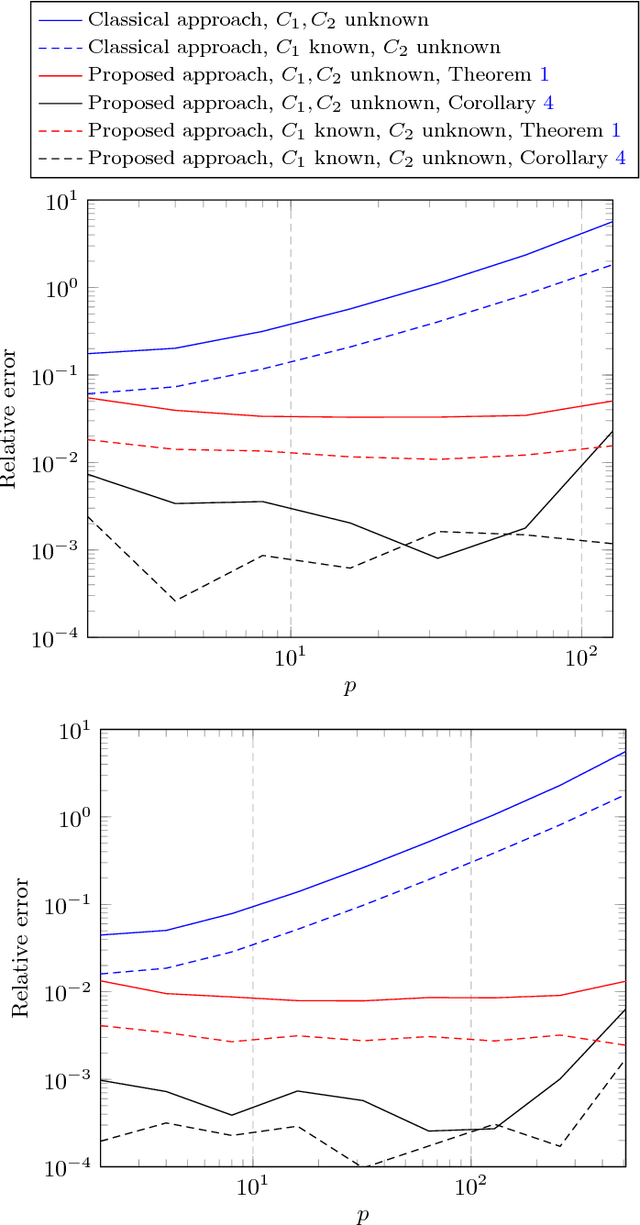
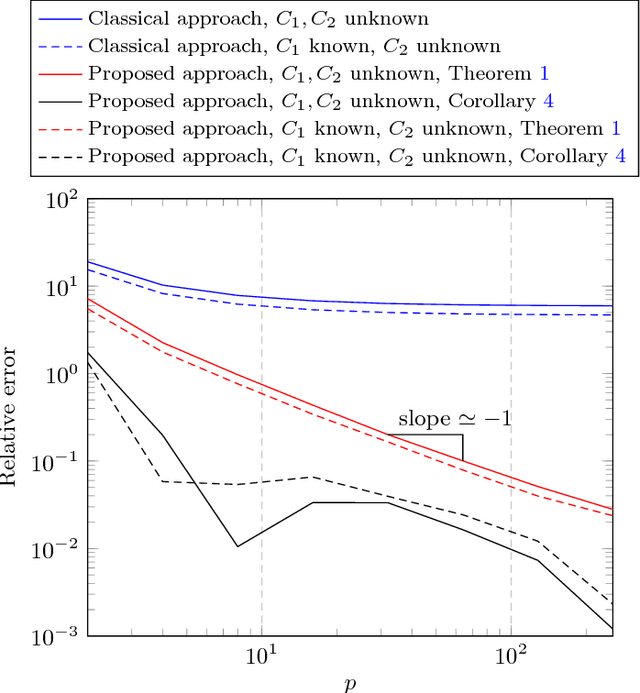
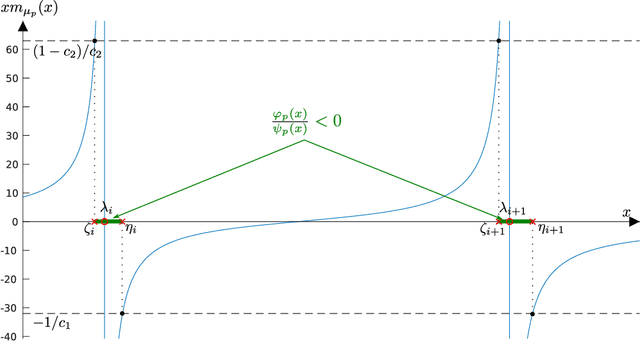
Given two sets $x_1^{(1)},\ldots,x_{n_1}^{(1)}$ and $x_1^{(2)},\ldots,x_{n_2}^{(2)}\in\mathbb{R}^p$ (or $\mathbb{C}^p$) of random vectors with zero mean and positive definite covariance matrices $C_1$ and $C_2\in\mathbb{R}^{p\times p}$ (or $\mathbb{C}^{p\times p}$), respectively, this article provides novel estimators for a wide range of distances between $C_1$ and $C_2$ (along with divergences between some zero mean and covariance $C_1$ or $C_2$ probability measures) of the form $\frac1p\sum_{i=1}^n f(\lambda_i(C_1^{-1}C_2))$ (with $\lambda_i(X)$ the eigenvalues of matrix $X$). These estimators are derived using recent advances in the field of random matrix theory and are asymptotically consistent as $n_1,n_2,p\to\infty$ with non trivial ratios $p/n_1<1$ and $p/n_2<1$ (the case $p/n_2>1$ is also discussed). A first "generic" estimator, valid for a large set of $f$ functions, is provided under the form of a complex integral. Then, for a selected set of $f$'s of practical interest (namely, $f(t)=t$, $f(t)=\log(t)$, $f(t)=\log(1+st)$ and $f(t)=\log^2(t)$), a closed-form expression is provided. Beside theoretical findings, simulation results suggest an outstanding performance advantage for the proposed estimators when compared to the classical "plug-in" estimator $\frac1p\sum_{i=1}^n f(\lambda_i(\hat C_1^{-1}\hat C_2))$ (with $\hat C_a=\frac1{n_a}\sum_{i=1}^{n_a}x_i^{(a)}x_i^{(a){\sf T}}$), and this even for very small values of $n_1,n_2,p$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge