A Study of Continuous Vector Representationsfor Theorem Proving

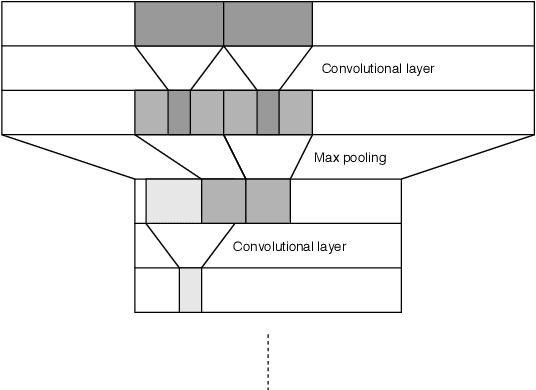
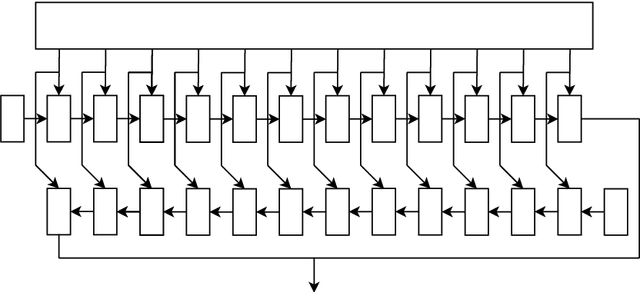
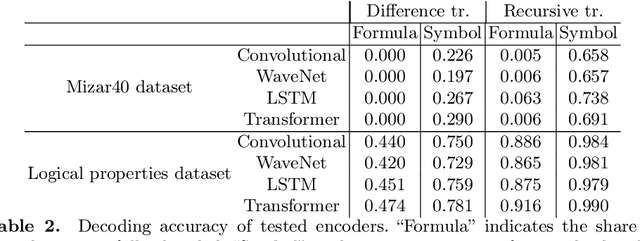
Applying machine learning to mathematical terms and formulas requires a suitable representation of formulas that is adequate for AI methods. In this paper, we develop an encoding that allows for logical properties to be preserved and is additionally reversible. This means that the tree shape of a formula including all symbols can be reconstructed from the dense vector representation. We do that by training two decoders: one that extracts the top symbol of the tree and one that extracts embedding vectors of subtrees. The syntactic and semantic logical properties that we aim to reserve include both structural formula properties, applicability of natural deduction steps, and even more complex operations like unifiability. We propose datasets that can be used to train these syntactic and semantic properties. We evaluate the viability of the developed encoding across the proposed datasets as well as for the practical theorem proving problem of premise selection in the Mizar corpus.

Improving Expressivity of Graph Neural Networks

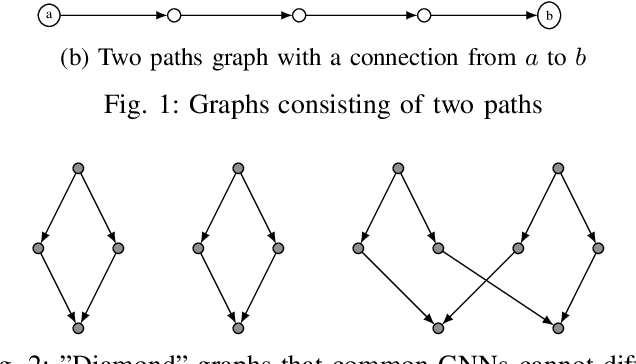
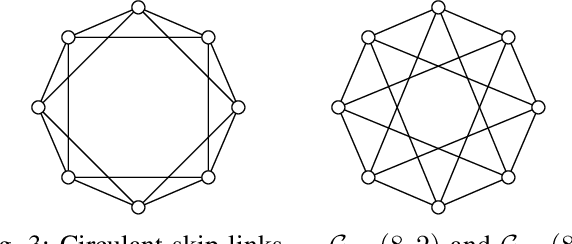
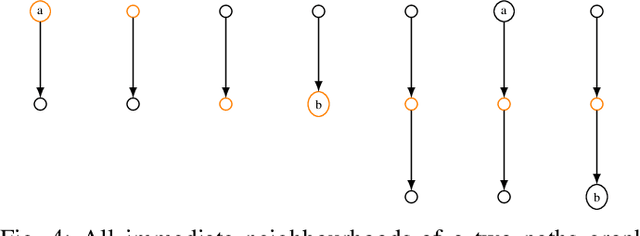
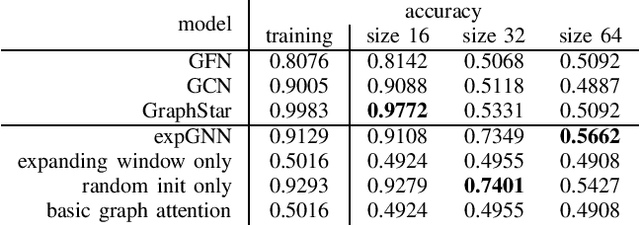
We propose a Graph Neural Network with greater expressive power than commonly used GNNs - not constrained to only differentiate between graphs that Weisfeiler-Lehman test recognizes to be non-isomorphic. We use a graph attention network with expanding attention window that aggregates information from nodes exponentially far away. We also use partially random initial embeddings, allowing differentiation between nodes that would otherwise look the same. This could cause problem with a traditional dropout mechanism, therefore we use a "head dropout", randomly ignoring some attention heads rather than some dimensions of the embedding.