A Bootstrap-based Inference Framework for Testing Similarity of Paired Networks

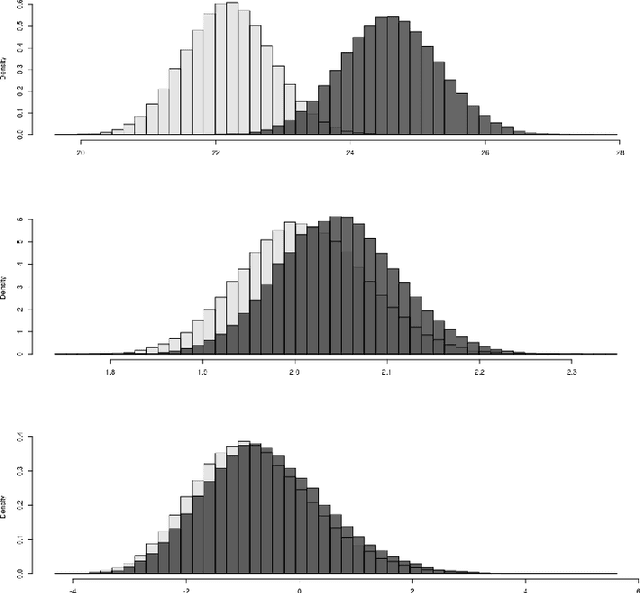
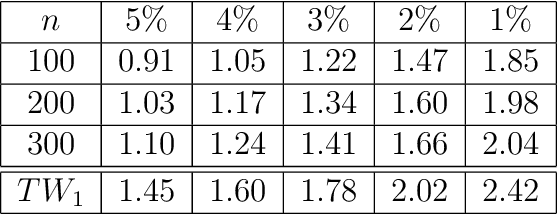
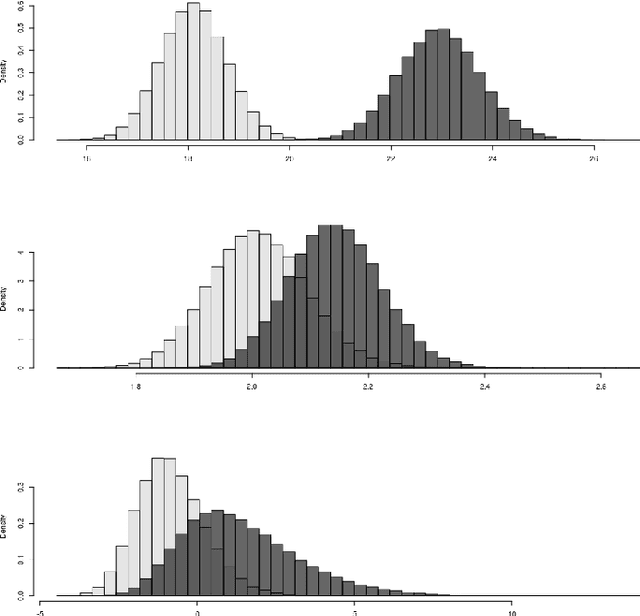
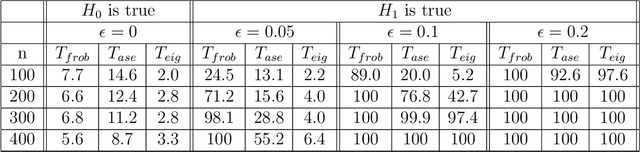
We live in an interconnected world where network valued data arises in many domains, and, fittingly, statistical network analysis has emerged as an active area in the literature. However, the topic of inference in networks has received relatively less attention. In this work, we consider the paired network inference problem where one is given two networks on the same set of nodes, and the goal is to test whether the given networks are stochastically similar in terms of some notion of similarity. We develop a general inferential framework based on parametric bootstrap to address this problem. Under this setting, we address two specific and important problems: the equality problem, i.e., whether the two networks are generated from the same random graph model, and the scaling problem, i.e., whether the underlying probability matrices of the two random graph models are scaled versions of each other.

Anomaly detection in static networks using egonets

Network data has rapidly emerged as an important and active area of statistical methodology. In this paper we consider the problem of anomaly detection in networks. Given a large background network, we seek to detect whether there is a small anomalous subgraph present in the network, and if such a subgraph is present, which nodes constitute the subgraph. We propose an inferential tool based on egonets to answer this question. The proposed method is computationally efficient and naturally amenable to parallel computing, and easily extends to a wide variety of network models. We demonstrate through simulation studies that the egonet method works well under a wide variety of network models. We obtain some fascinating empirical results by applying the egonet method on several well-studied benchmark datasets.