Adversarially-Robust TD Learning with Markovian Data: Finite-Time Rates and Fundamental Limits

One of the most basic problems in reinforcement learning (RL) is policy evaluation: estimating the long-term return, i.e., value function, corresponding to a given fixed policy. The celebrated Temporal Difference (TD) learning algorithm addresses this problem, and recent work has investigated finite-time convergence guarantees for this algorithm and variants thereof. However, these guarantees hinge on the reward observations being always generated from a well-behaved (e.g., sub-Gaussian) true reward distribution. Motivated by harsh, real-world environments where such an idealistic assumption may no longer hold, we revisit the policy evaluation problem from the perspective of adversarial robustness. In particular, we consider a Huber-contaminated reward model where an adversary can arbitrarily corrupt each reward sample with a small probability $\epsilon$. Under this observation model, we first show that the adversary can cause the vanilla TD algorithm to converge to any arbitrary value function. We then develop a novel algorithm called Robust-TD and prove that its finite-time guarantees match that of vanilla TD with linear function approximation up to a small $O(\epsilon)$ term that captures the effect of corruption. We complement this result with a minimax lower bound, revealing that such an additive corruption-induced term is unavoidable. To our knowledge, these results are the first of their kind in the context of adversarial robustness of stochastic approximation schemes driven by Markov noise. The key new technical tool that enables our results is an analysis of the Median-of-Means estimator with corrupted, time-correlated data that might be of independent interest to the literature on robust statistics.

Robust Q-Learning under Corrupted Rewards

Recently, there has been a surge of interest in analyzing the non-asymptotic behavior of model-free reinforcement learning algorithms. However, the performance of such algorithms in non-ideal environments, such as in the presence of corrupted rewards, is poorly understood. Motivated by this gap, we investigate the robustness of the celebrated Q-learning algorithm to a strong-contamination attack model, where an adversary can arbitrarily perturb a small fraction of the observed rewards. We start by proving that such an attack can cause the vanilla Q-learning algorithm to incur arbitrarily large errors. We then develop a novel robust synchronous Q-learning algorithm that uses historical reward data to construct robust empirical Bellman operators at each time step. Finally, we prove a finite-time convergence rate for our algorithm that matches known state-of-the-art bounds (in the absence of attacks) up to a small inevitable $O(\varepsilon)$ error term that scales with the adversarial corruption fraction $\varepsilon$. Notably, our results continue to hold even when the true reward distributions have infinite support, provided they admit bounded second moments.

Fragile object transportation by a multi-robot system in an unknown environment using a semi-decentralized control approach

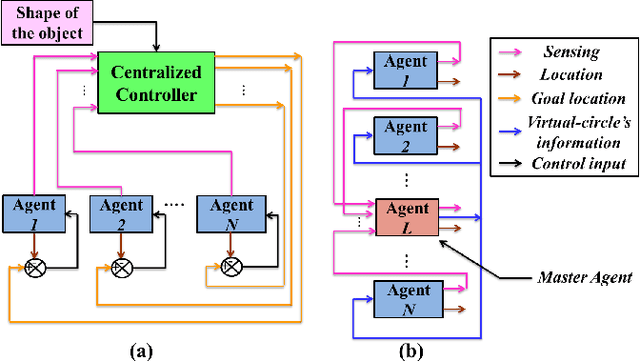
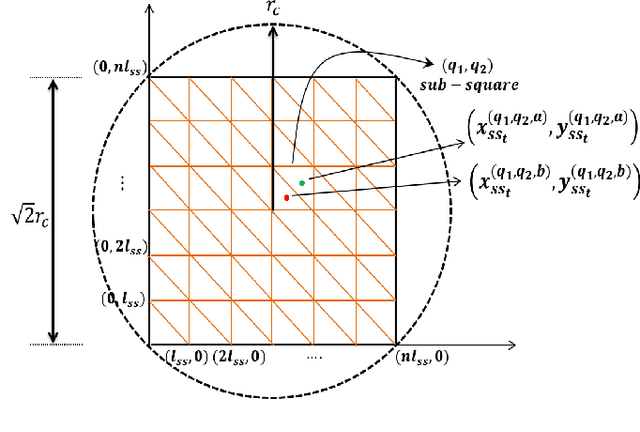
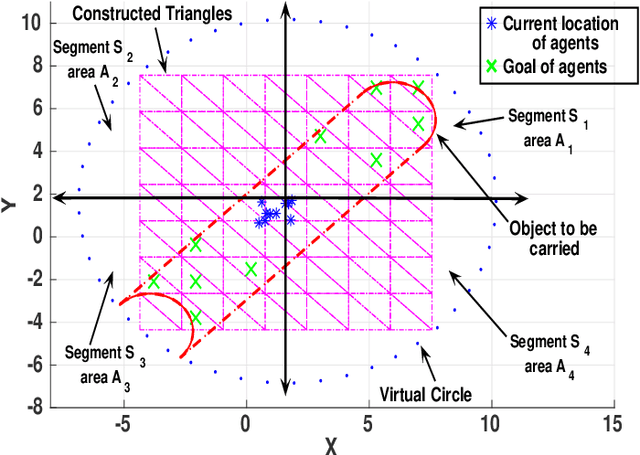
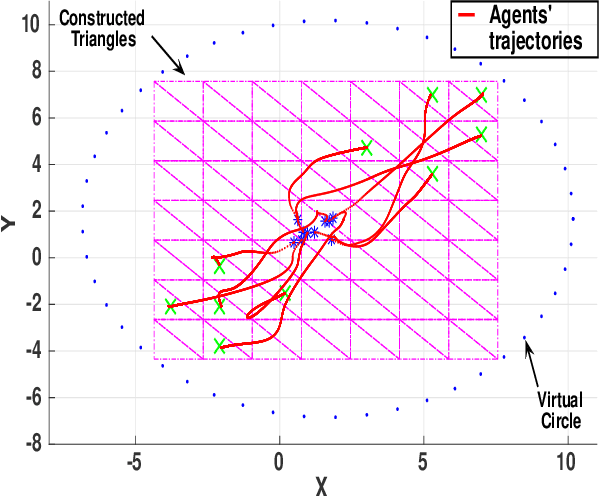
In this paper, we introduce a semi-decentralized control technique for a swarm of robots transporting a fragile object to a destination in an uncertain occluded environment.The proposed approach has been split into two parts. The initial part (Phase 1) includes a centralized control strategy for creating a specific formation among the agents so that the object to be transported, can be positioned properly on the top of the system. We present a novel triangle packing scheme fused with a circular region-based shape control method for creating a rigid configuration among the robots. In the later part (Phase 2), the swarm system is required to convey the object to the destination in a decentralized way employing the region based shape control approach. The simulation result as well as the comparison study demonstrates the effectiveness of our proposed scheme.