Dynamic Calibration of Nonlinear Sensors with Time-Drifts and Delays by Bayesian Inference

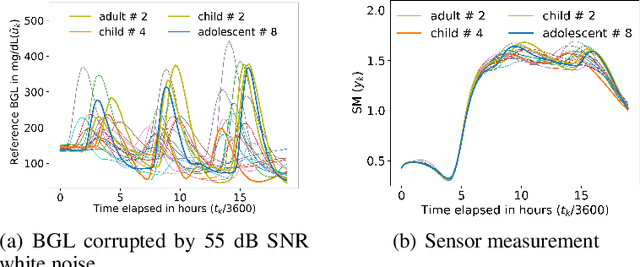
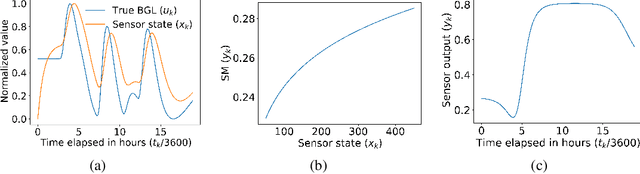
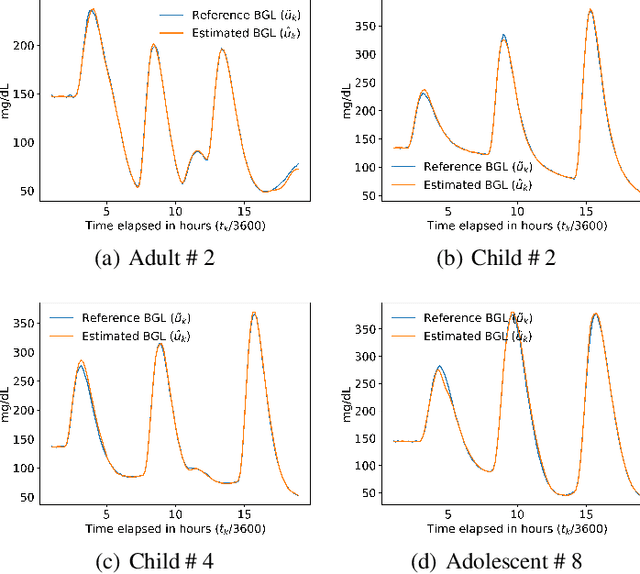
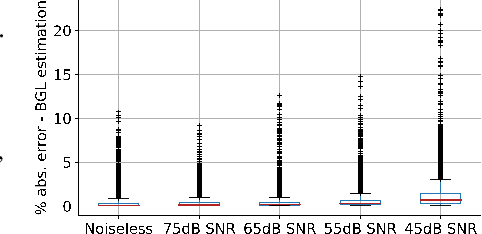
Most sensor calibrations rely on the linearity and steadiness of their response characteristics, but practical sensors are nonlinear, and their response drifts with time, restricting their choices for adoption. To broaden the realm of sensors to allow nonlinearity and time-drift in the underlying dynamics, a Bayesian inference-based nonlinear, non-causal dynamic calibration method is introduced, where the sensed value is estimated as a posterior conditional mean given a finite-length sequence of the sensor measurements and the elapsed time. Additionally, an algorithm is proposed to adjust an already learned calibration map online whenever new data arrives. The effectiveness of the proposed method is validated on continuous-glucose-monitoring (CGM) data from an alive rat equipped with an in-house optical glucose sensor. To allow flexibility in choice, the validation is also performed on a synthetic blood glucose level (BGL) dataset generated using FDA-approved virtual diabetic patient models together with an illustrative CGM sensor model.

Robust Stability of Neural-Network Controlled Nonlinear Systems with Parametric Variability

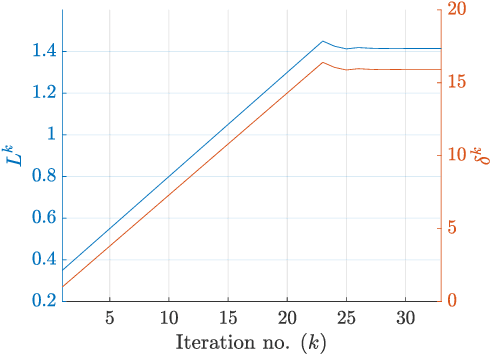
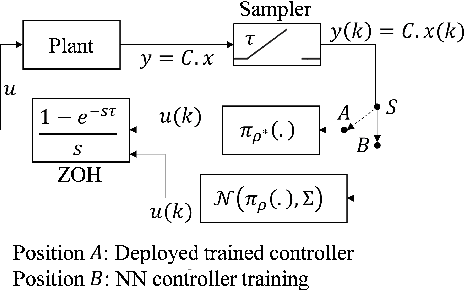
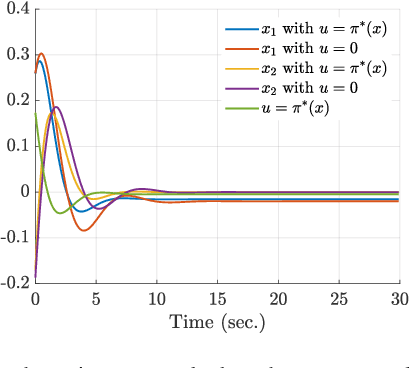
Stability certification and identification of the stabilizable operating region of a system are two important concerns to ensure its operational safety/security and robustness. With the advent of machine-learning tools, these issues are specially important for systems with machine-learned components in the feedback loop. Here we develop a theory for stability and stabilizability of a class of neural-network controlled nonlinear systems, where the equilibria can drift when parametric changes occur. A Lyapunov based convex stability certificate is developed and is further used to devise an estimate for a local Lipschitz upper bound for a neural-network (NN) controller and a corresponding operating domain on the state space, containing an initialization set from where the closed-loop (CL) local asymptotic stability of each system in the class is guaranteed under the same controller, while the system trajectories remain confined to the operating domain. For computing such a robust stabilizing NN controller, a stability guaranteed training (SGT) algorithm is also proposed. The effectiveness of the proposed framework is demonstrated using illustrative examples.