Soroush Aramideh
Monotone Tree-Based GAMI Models by Adapting XGBoost
Sep 05, 2023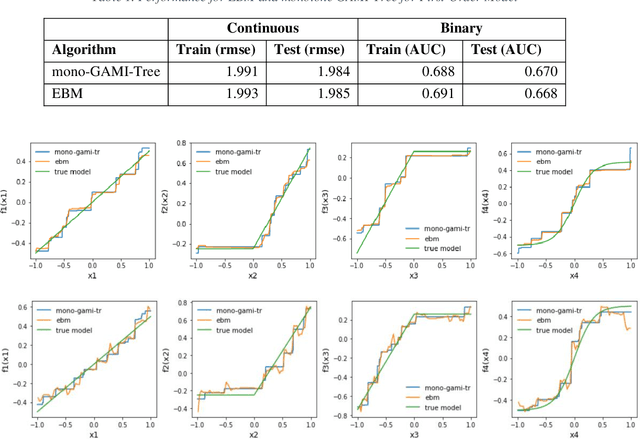
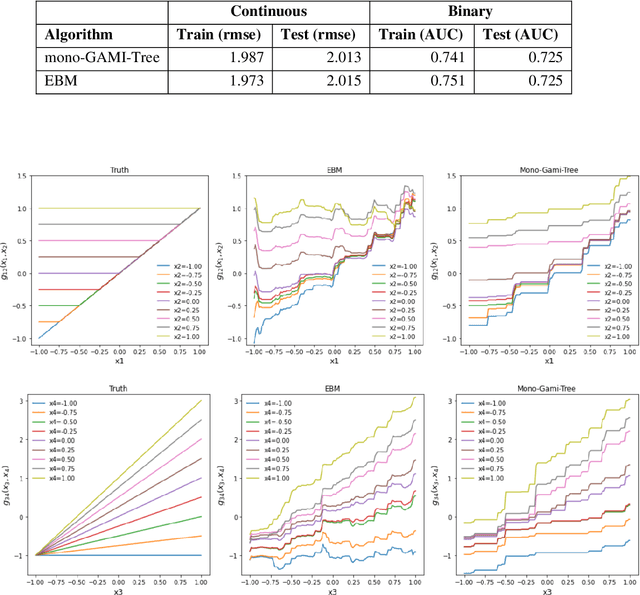
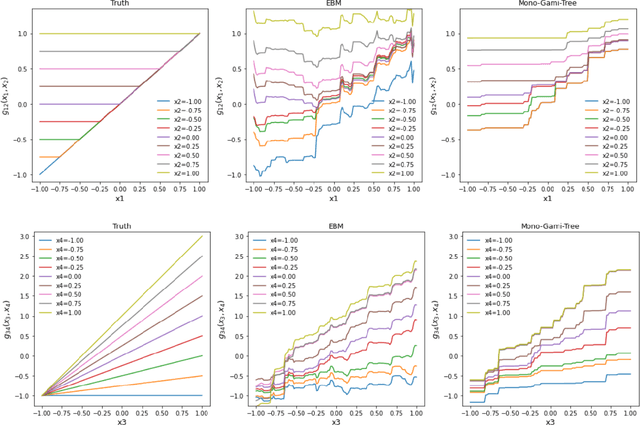
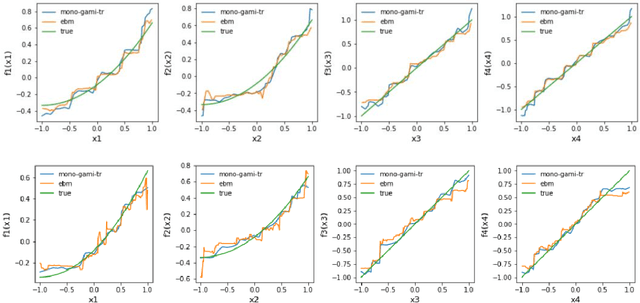
Abstract:Recent papers have used machine learning architecture to fit low-order functional ANOVA models with main effects and second-order interactions. These GAMI (GAM + Interaction) models are directly interpretable as the functional main effects and interactions can be easily plotted and visualized. Unfortunately, it is not easy to incorporate the monotonicity requirement into the existing GAMI models based on boosted trees, such as EBM (Lou et al. 2013) and GAMI-Lin-T (Hu et al. 2022). This paper considers models of the form $f(x)=\sum_{j,k}f_{j,k}(x_j, x_k)$ and develops monotone tree-based GAMI models, called monotone GAMI-Tree, by adapting the XGBoost algorithm. It is straightforward to fit a monotone model to $f(x)$ using the options in XGBoost. However, the fitted model is still a black box. We take a different approach: i) use a filtering technique to determine the important interactions, ii) fit a monotone XGBoost algorithm with the selected interactions, and finally iii) parse and purify the results to get a monotone GAMI model. Simulated datasets are used to demonstrate the behaviors of mono-GAMI-Tree and EBM, both of which use piecewise constant fits. Note that the monotonicity requirement is for the full model. Under certain situations, the main effects will also be monotone. But, as seen in the examples, the interactions will not be monotone.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge