Optimal Multilayered Motion Planning for Multiple Differential Drive Mobile Robots with Hierarchical Prioritization (OM-MP)

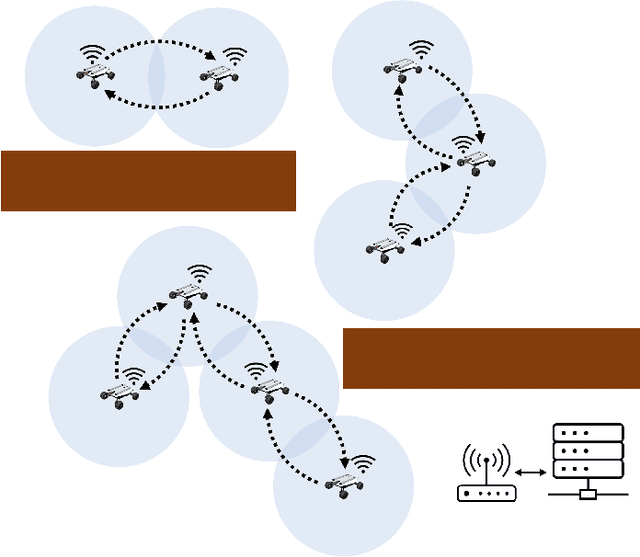
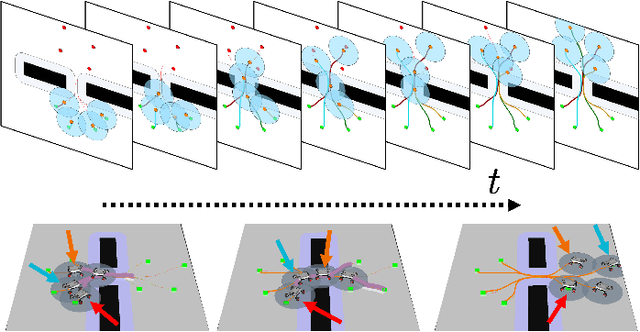
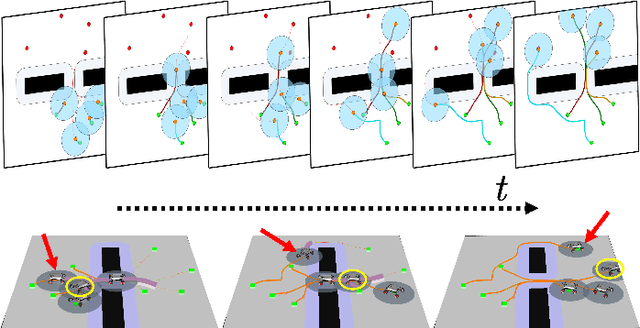
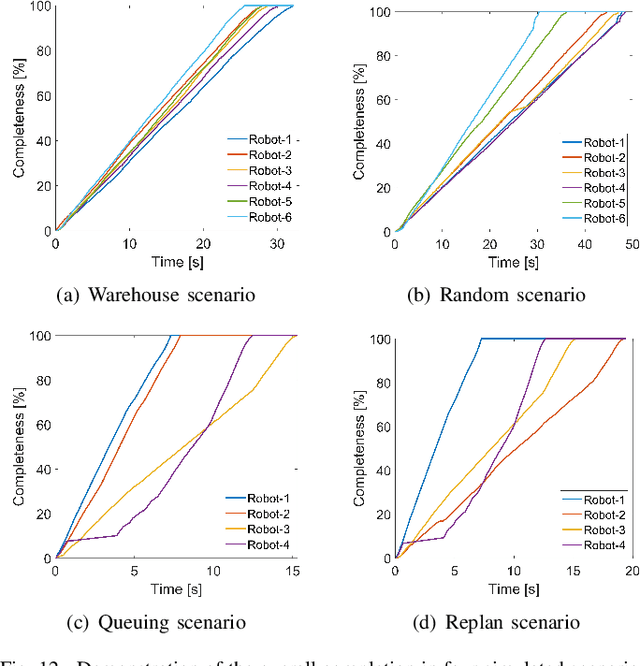
We present a novel framework for addressing the challenges of multi-Agent planning and formation control within intricate and dynamic environments. This framework transforms the Multi-Agent Path Finding (MAPF) problem into a Multi-Agent Trajectory Planning (MATP) problem. Unlike traditional MAPF solutions, our multilayer optimization scheme consists of a global planner optimization solver, which is dedicated to determining concise global paths for each individual robot, and a local planner with an embedded optimization solver aimed at ensuring the feasibility of local robot trajectories. By implementing a hierarchical prioritization strategy, we enhance robots' efficiency and approximate the global optimal solution. Specifically, within the global planner, we employ the Augmented Graph Search (AGS) algorithm, which significantly improves the speed of solutions. Meanwhile, within the local planner optimization solver, we utilize Control Barrier functions (CBFs) and introduced an oblique cylindrical obstacle bounding box based on the time axis for obstacle avoidance and construct a single-robot locally aware-communication circle to ensure the simplicity, speed, and accuracy of locally optimized solutions. Additionally, we integrate the weight and priority of path traces to prevent deadlocks in limiting scenarios. Compared to the other state-of-the-art methods, including CBS, ECBS and other derivative algorithms, our proposed method demonstrates superior performance in terms of capacity, flexible scalability and overall task optimality in theory, as validated through simulations and experiments.

Fast Safe Rectangular Corridor-based Online AGV Trajectory Optimization with Obstacle Avoidance

Automated Guided Vehicles (AGVs) are widely adopted in various industries due to their efficiency and adaptability. However, safely deploying AGVs in dynamic environments remains a significant challenge. This paper introduces an online trajectory optimization framework, the Fast Safe Rectangular Corridor (FSRC), designed for AGVs in obstacle-rich settings. The primary challenge is efficiently planning trajectories that prioritize safety and collision avoidance. To tackle this challenge, the FSRC algorithm constructs convex regions, represented as rectangular corridors, to address obstacle avoidance constraints within an optimal control problem. This conversion from non-convex to box constraints improves the collision avoidance efficiency and quality. Additionally, the Modified Visibility Graph algorithm speeds up path planning, and a boundary discretization strategy expedites FSRC construction. The framework also includes a dynamic obstacle avoidance strategy for real-time adaptability. Our framework's effectiveness and superiority have been demonstrated in experiments, particularly in computational efficiency (see Fig. \ref{fig:case1} and \ref{fig:case23}). Compared to state-of-the-art frameworks, our trajectory planning framework significantly enhances computational efficiency, ranging from 1 to 2 orders of magnitude (see Table \ref{tab:res}). Notably, the FSRC algorithm outperforms other safe convex corridor-based methods, substantially improving computational efficiency by 1 to 2 orders of magnitude (see Table \ref{tab:FRSC}).