On multi-class learning through the minimization of the confusion matrix norm

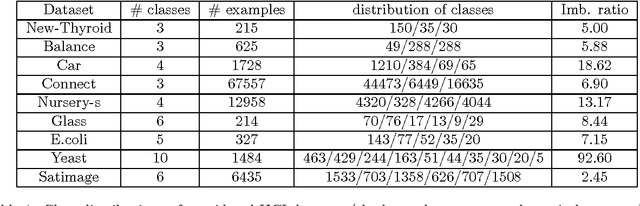
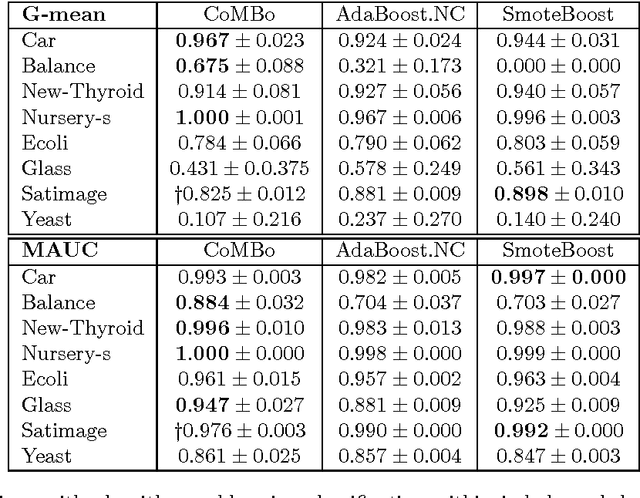
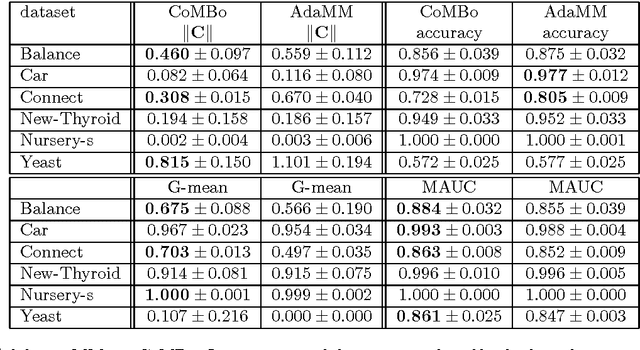
In imbalanced multi-class classification problems, the misclassification rate as an error measure may not be a relevant choice. Several methods have been developed where the performance measure retained richer information than the mere misclassification rate: misclassification costs, ROC-based information, etc. Following this idea of dealing with alternate measures of performance, we propose to address imbalanced classification problems by using a new measure to be optimized: the norm of the confusion matrix. Indeed, recent results show that using the norm of the confusion matrix as an error measure can be quite interesting due to the fine-grain informations contained in the matrix, especially in the case of imbalanced classes. Our first contribution then consists in showing that optimizing criterion based on the confusion matrix gives rise to a common background for cost-sensitive methods aimed at dealing with imbalanced classes learning problems. As our second contribution, we propose an extension of a recent multi-class boosting method --- namely AdaBoost.MM --- to the imbalanced class problem, by greedily minimizing the empirical norm of the confusion matrix. A theoretical analysis of the properties of the proposed method is presented, while experimental results illustrate the behavior of the algorithm and show the relevancy of the approach compared to other methods.

PAC-Bayesian Generalization Bound on Confusion Matrix for Multi-Class Classification

In this work, we propose a PAC-Bayes bound for the generalization risk of the Gibbs classifier in the multi-class classification framework. The novelty of our work is the critical use of the confusion matrix of a classifier as an error measure; this puts our contribution in the line of work aiming at dealing with performance measure that are richer than mere scalar criterion such as the misclassification rate. Thanks to very recent and beautiful results on matrix concentration inequalities, we derive two bounds showing that the true confusion risk of the Gibbs classifier is upper-bounded by its empirical risk plus a term depending on the number of training examples in each class. To the best of our knowledge, this is the first PAC-Bayes bounds based on confusion matrices.