Classification Using Global and Local Mahalanobis Distances

We propose a novel semi-parametric classifier based on Mahalanobis distances of an observation from the competing classes. Our tool is a generalized additive model with the logistic link function that uses these distances as features to estimate the posterior probabilities of the different classes. While popular parametric classifiers like linear and quadratic discriminant analyses are mainly motivated by the normality of the underlying distributions, the proposed classifier is more flexible and free from such parametric assumptions. Since the densities of elliptic distributions are functions of Mahalanobis distances, this classifier works well when the competing classes are (nearly) elliptic. In such cases, it often outperforms popular nonparametric classifiers, especially when the sample size is small compared to the dimension of the data. To cope with non-elliptic and possibly multimodal distributions, we propose a local version of the Mahalanobis distance. Subsequently, we propose another classifier based on a generalized additive model that uses the local Mahalanobis distances as features. This nonparametric classifier usually performs like the Mahalanobis distance based semiparametric classifier when the underlying distributions are elliptic, but outperforms it for several non-elliptic and multimodal distributions. We also investigate the behaviour of these two classifiers in high dimension, low sample size situations. A thorough numerical study involving several simulated and real datasets demonstrate the usefulness of the proposed classifiers in comparison to many state-of-the-art methods.

CovNet: Covariance Networks for Functional Data on Multidimensional Domains

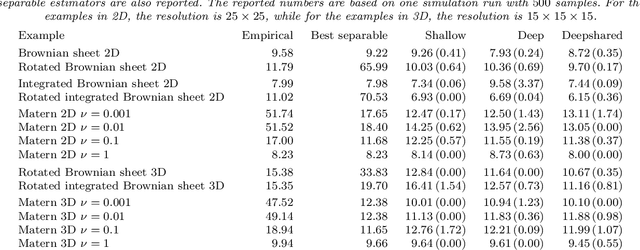
Covariance estimation is ubiquitous in functional data analysis. Yet, the case of functional observations over multidimensional domains introduces computational and statistical challenges, rendering the standard methods effectively inapplicable. To address this problem, we introduce Covariance Networks (CovNet) as a modeling and estimation tool. The CovNet model is universal -- it can be used to approximate any covariance up to desired precision. Moreover, the model can be fitted efficiently to the data and its neural network architecture allows us to employ modern computational tools in the implementation. The CovNet model also admits a closed-form eigen-decomposition, which can be computed efficiently, without constructing the covariance itself. This facilitates easy storage and subsequent manipulation in the context of the CovNet. Moreover, we establish consistency of the proposed estimator and derive its rate of convergence. The usefulness of the proposed method is demonstrated by means of an extensive simulation study.

On a Generalization of the Average Distance Classifier

In high dimension, low sample size (HDLSS)settings, the simple average distance classifier based on the Euclidean distance performs poorly if differences between the locations get masked by the scale differences. To rectify this issue, modifications to the average distance classifier was proposed by Chan and Hall (2009). However, the existing classifiers cannot discriminate when the populations differ in other aspects than locations and scales. In this article, we propose some simple transformations of the average distance classifier to tackle this issue. The resulting classifiers perform quite well even when the underlying populations have the same location and scale. The high-dimensional behaviour of the proposed classifiers is studied theoretically. Numerical experiments with a variety of simulated as well as real data sets exhibit the usefulness of the proposed methodology.