Likelihood Ratio Tests by Kernel Gaussian Embedding

We propose a novel kernel-based nonparametric two-sample test, employing the combined use of kernel mean and kernel covariance embedding. Our test builds on recent results showing how such combined embeddings map distinct probability measures to mutually singular Gaussian measures on the kernel's RKHS. Leveraging this result, we construct a test statistic based on the relative entropy between the Gaussian embeddings, i.e.\ the likelihood ratio. The likelihood ratio is specifically tailored to detect equality versus singularity of two Gaussians, and satisfies a ``$0/\infty$" law, in that it vanishes under the null and diverges under the alternative. To implement the test in finite samples, we introduce a regularised version, calibrated by way of permutation. We prove consistency, establish uniform power guarantees under mild conditions, and discuss how our framework unifies and extends prior approaches based on spectrally regularized MMD. Empirical results on synthetic and real data demonstrate remarkable gains in power compared to state-of-the-art methods, particularly in high-dimensional and weak-signal regimes.

From Two Sample Testing to Singular Gaussian Discrimination

We establish that testing for the equality of two probability measures on a general separable and compact metric space is equivalent to testing for the singularity between two corresponding Gaussian measures on a suitable Reproducing Kernel Hilbert Space. The corresponding Gaussians are defined via the notion of kernel mean and covariance embedding of a probability measure. Discerning two singular Gaussians is fundamentally simpler from an information-theoretic perspective than non-parametric two-sample testing, particularly in high-dimensional settings. Our proof leverages the Feldman-Hajek criterion for singularity/equivalence of Gaussians on Hilbert spaces, and shows that discrepancies between distributions are heavily magnified through their corresponding Gaussian embeddings: at a population level, distinct probability measures lead to essentially separated Gaussian embeddings. This appears to be a new instance of the blessing of dimensionality that can be harnessed for the design of efficient inference tools in great generality.

Computerized Tomography and Reproducing Kernels

The X-ray transform is one of the most fundamental integral operators in image processing and reconstruction. In this article, we revisit its mathematical formalism, and propose an innovative approach making use of Reproducing Kernel Hilbert Spaces (RKHS). Within this framework, the X-ray transform can be considered as a natural analogue of Euclidean projections. The RKHS framework considerably simplifies projection image interpolation, and leads to an analogue of the celebrated representer theorem for the problem of tomographic reconstruction. It leads to methodology that is dimension-free and stands apart from conventional filtered back-projection techniques, as it does not hinge on the Fourier transform. It also allows us to establish sharp stability results at a genuinely functional level, but in the realistic setting where the data are discrete and noisy. The RKHS framework is amenable to any reproducing kernel on a unit ball, affording a high level of generality. When the kernel is chosen to be rotation-invariant, one can obtain explicit spectral representations which elucidate the regularity structure of the associated Hilbert spaces, and one can also solve the reconstruction problem at the same computational cost as filtered back-projection.

CovNet: Covariance Networks for Functional Data on Multidimensional Domains

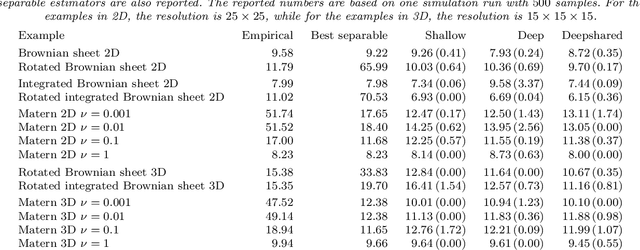
Covariance estimation is ubiquitous in functional data analysis. Yet, the case of functional observations over multidimensional domains introduces computational and statistical challenges, rendering the standard methods effectively inapplicable. To address this problem, we introduce Covariance Networks (CovNet) as a modeling and estimation tool. The CovNet model is universal -- it can be used to approximate any covariance up to desired precision. Moreover, the model can be fitted efficiently to the data and its neural network architecture allows us to employ modern computational tools in the implementation. The CovNet model also admits a closed-form eigen-decomposition, which can be computed efficiently, without constructing the covariance itself. This facilitates easy storage and subsequent manipulation in the context of the CovNet. Moreover, we establish consistency of the proposed estimator and derive its rate of convergence. The usefulness of the proposed method is demonstrated by means of an extensive simulation study.