Causal Model Analysis using Collider v-structure with Negative Percentage Mapping

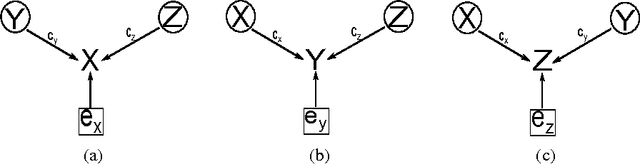
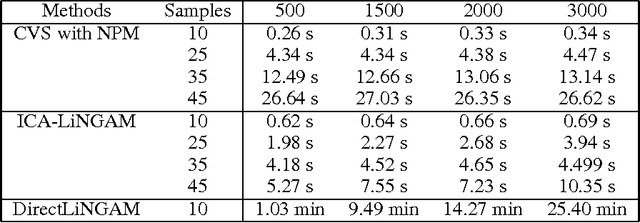
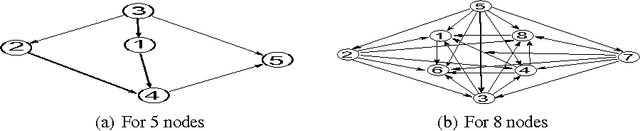
A major problem of causal inference is the arrangement of dependent nodes in a directed acyclic graph (DAG) with path coefficients and observed confounders. Path coefficients do not provide the units to measure the strength of information flowing from one node to the other. Here we proposed the method of causal structure learning using collider v-structures (CVS) with Negative Percentage Mapping (NPM) to get selective thresholds of information strength, to direct the edges and subjective confounders in a DAG. The NPM is used to scale the strength of information passed through nodes in units of percentage from interval from 0 to 1. The causal structures are constructed by bottom up approach using path coefficients, causal directions and confounders, derived implementing collider v-structure and NPM. The method is self-sufficient to observe all the latent confounders present in the causal model and capable of detecting every responsible causal direction. The results are tested for simulated datasets of non-Gaussian distributions and compared with DirectLiNGAM and ICA-LiNGAM to check efficiency of the proposed method.

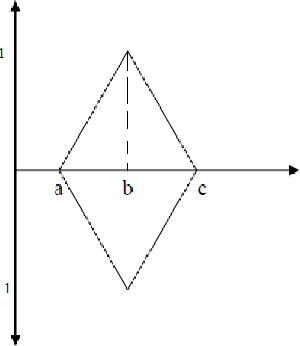
Pseudo Fuzzy Set

Here a novel idea to handle imprecise or vague set viz. Pseudo fuzzy set has been proposed. Pseudo fuzzy set is a triplet of element and its two membership functions. Both the membership functions may or may not be dependent. The hypothesis is that every positive sense has some negative sense. So, one membership function has been considered as positive and another as negative. Considering this concept, here the development of Pseudo fuzzy set and its property along with Pseudo fuzzy numbers has been discussed.

Numerical Solution of Fuzzy Stochastic Differential Equation

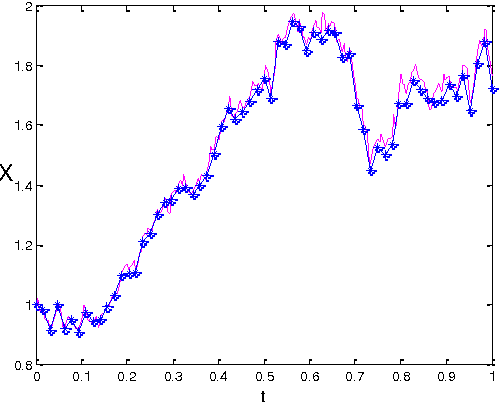
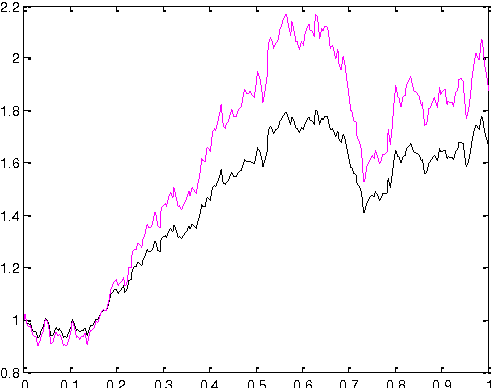
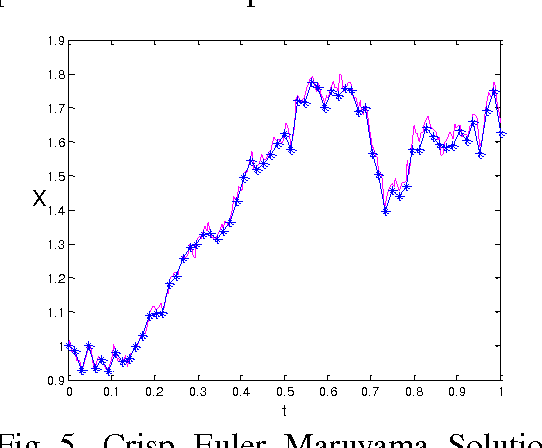
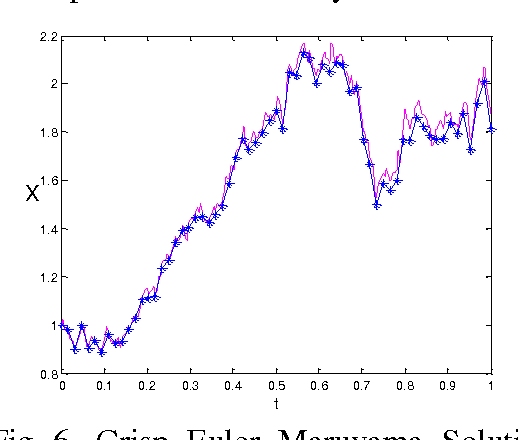
In this paper an alternative approach to solve uncertain Stochastic Differential Equation (SDE) is proposed. This uncertainty occurs due to the involved parameters in system and these are considered as Triangular Fuzzy Numbers (TFN). Here the proposed fuzzy arithmetic in [2] is used as a tool to handle Fuzzy Stochastic Differential Equation (FSDE). In particular, a system of Ito stochastic differential equations is analysed with fuzzy parameters. Further exact and Euler Maruyama approximation methods with fuzzy values are demonstrated and solved some standard SDE.

Fault Classification using Pseudomodal Energies and Neuro-fuzzy modelling

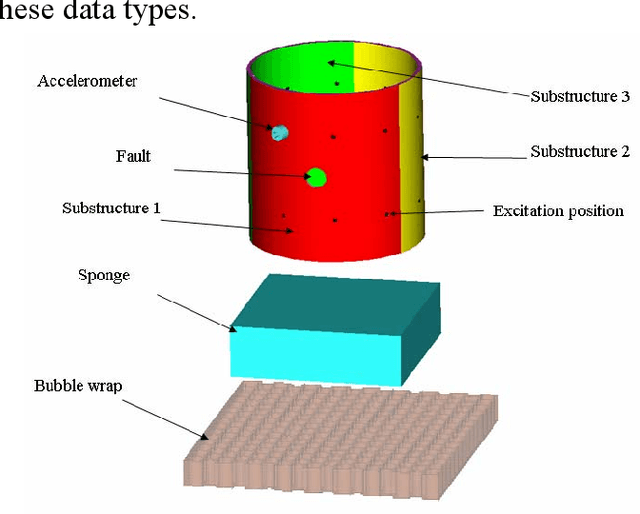
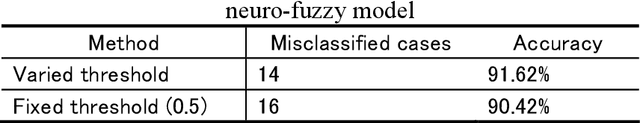
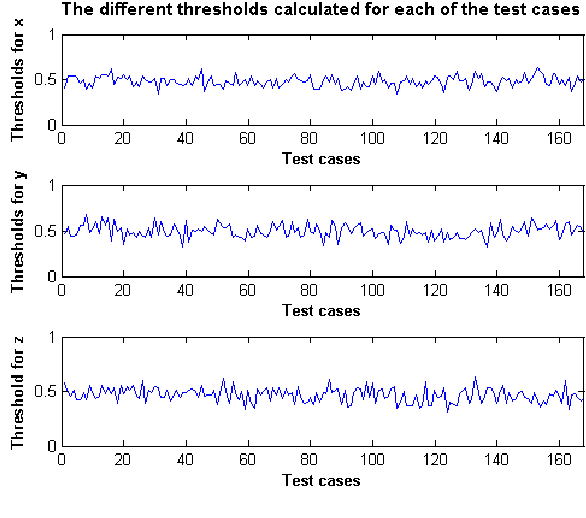
This paper presents a fault classification method which makes use of a Takagi-Sugeno neuro-fuzzy model and Pseudomodal energies calculated from the vibration signals of cylindrical shells. The calculation of Pseudomodal Energies, for the purposes of condition monitoring, has previously been found to be an accurate method of extracting features from vibration signals. This calculation is therefore used to extract features from vibration signals obtained from a diverse population of cylindrical shells. Some of the cylinders in the population have faults in different substructures. The pseudomodal energies calculated from the vibration signals are then used as inputs to a neuro-fuzzy model. A leave-one-out cross-validation process is used to test the performance of the model. It is found that the neuro-fuzzy model is able to classify faults with an accuracy of 91.62%, which is higher than the previously used multilayer perceptron.

Fault Classification in Cylinders Using Multilayer Perceptrons, Support Vector Machines and Guassian Mixture Models

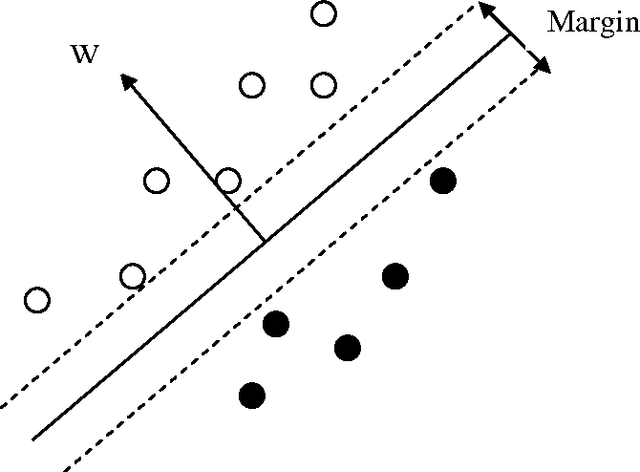
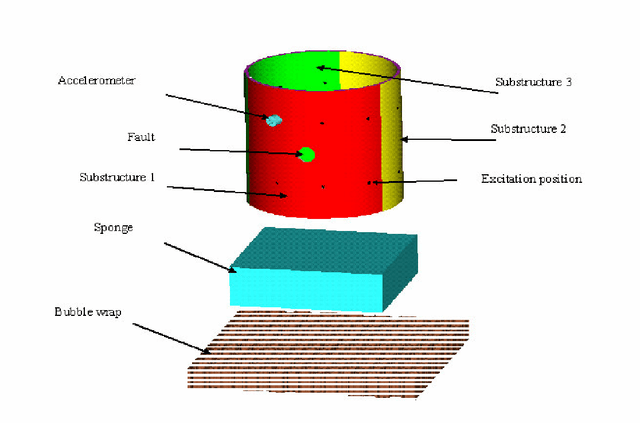
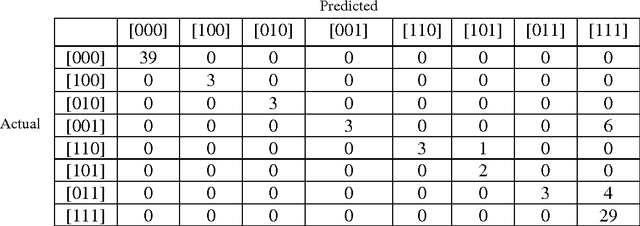
Gaussian mixture models (GMM) and support vector machines (SVM) are introduced to classify faults in a population of cylindrical shells. The proposed procedures are tested on a population of 20 cylindrical shells and their performance is compared to the procedure, which uses multi-layer perceptrons (MLP). The modal properties extracted from vibration data are used to train the GMM, SVM and MLP. It is observed that the GMM produces 98%, SVM produces 94% classification accuracy while the MLP produces 88% classification rates.