Data-driven geophysics: from dictionary learning to deep learning

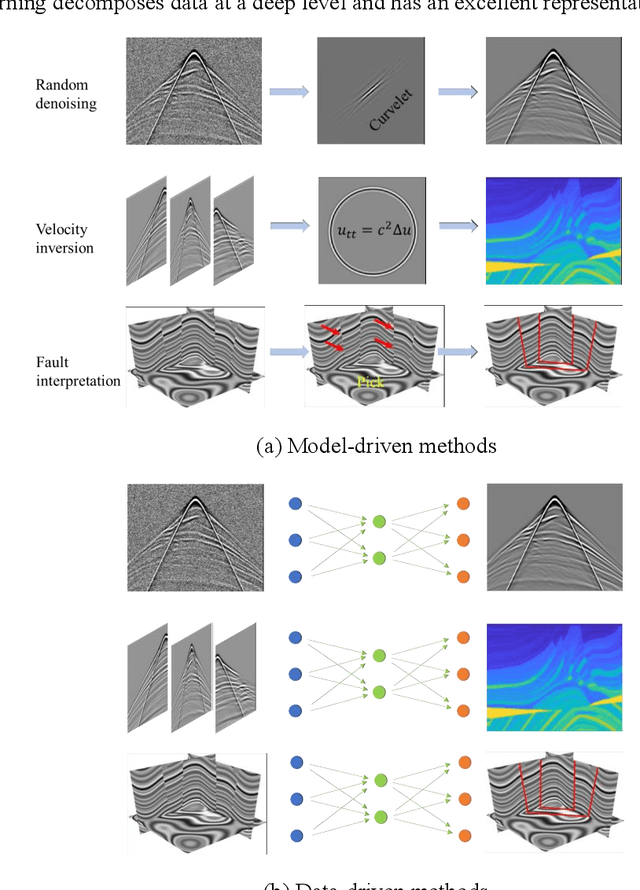
Understanding the principles of geophysical phenomena is an essential and challenging task. Model-driven approaches have supported the development of geophysics for a long time; however, such methods suffer from the curse of dimensionality and may inaccurately model the subsurface. Data-driven techniques may overcome these issues with increasingly available geophysical data. In this article, we review the basic concepts of and recent advances in data-driven approaches from dictionary learning to deep learning in a variety of geophysical scenarios, including seismic and earthquake data processing, inversion, and interpretation. We present a coding tutorial and a summary of tips for beginners and interested geophysical readers to rapidly explore deep learning. Some promising directions are provided for future research involving deep learning in geophysics, such as unsupervised learning, transfer learning, multimodal deep learning, federated learning, uncertainty estimation, and activate learning.

Deep learning tutorial for denoising

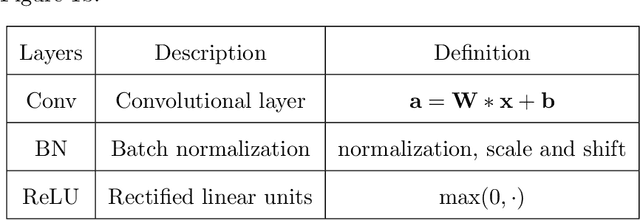
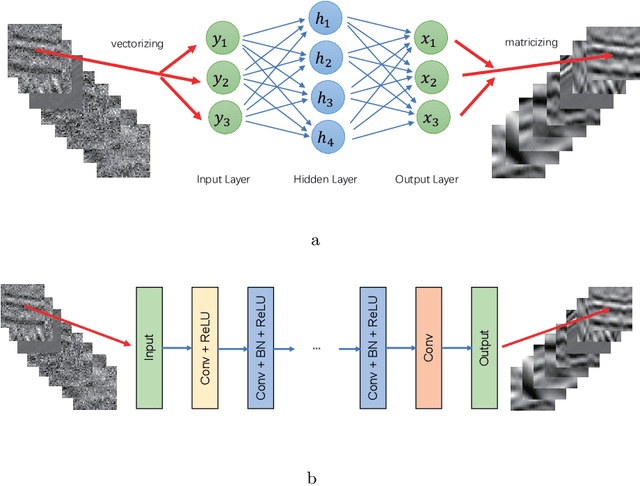
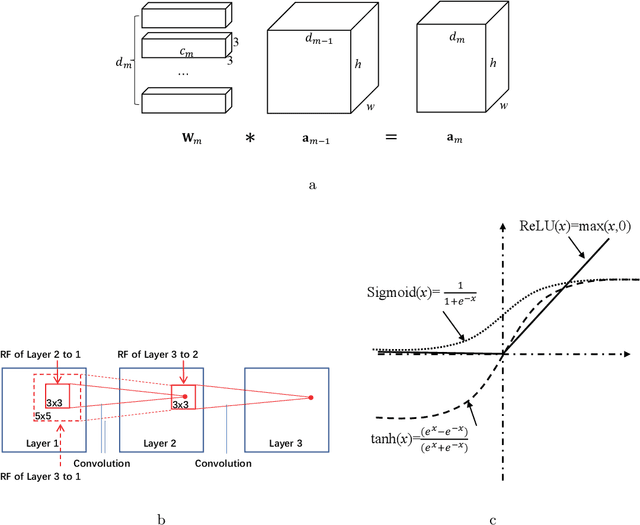
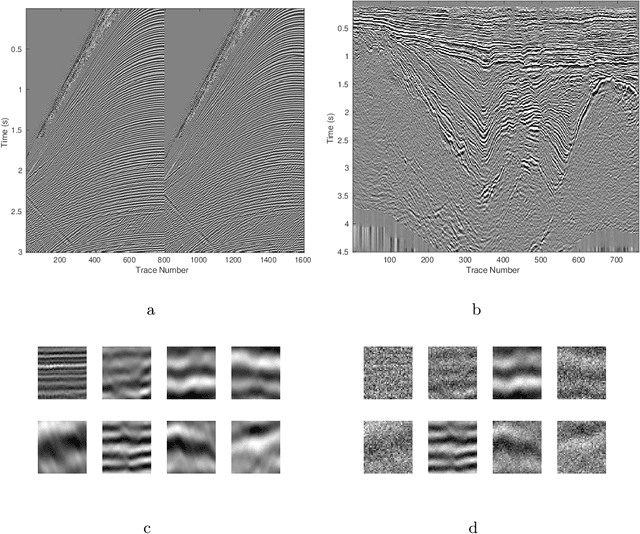
We herein introduce deep learning to seismic noise attenuation. Compared with traditional seismic noise attenuation algorithms that depend on signal models and their corresponding prior assumptions, a deep neural network is trained based on a large training set, where the inputs are the raw datasets and the corresponding outputs are the desired clean data. After the completion of training, the deep learning method achieves adaptive denoising with no requirements of (i) accurate modeling of the signal and noise, and (ii) optimal parameters tuning. We call this intelligent denoising. We use a convolutional neural network as the basic tool for deep learning. The training set is generated with manually added noise in random and linear noise attenuation, and with the wave equation in the multiple attenuation. Stochastic gradient descent is used to solve the optimal parameters for the convolutional neural network. The runtime of deep learning on a graphics processing unit for denoising has the same order as the $f-x$ deconvolutional method. Synthetic and field results show the potential applications of deep learning in the automation of random noise attenuation with unknown variance, linear noise, and multiples.