An Analysis Framework for Understanding Deep Neural Networks Based on Network Dynamics

Advancing artificial intelligence demands a deeper understanding of the mechanisms underlying deep learning. Here, we propose a straightforward analysis framework based on the dynamics of learning models. Neurons are categorized into two modes based on whether their transformation functions preserve order. This categorization reveals how deep neural networks (DNNs) maximize information extraction by rationally allocating the proportion of neurons in different modes across deep layers. We further introduce the attraction basins of the training samples in both the sample vector space and the weight vector space to characterize the generalization ability of DNNs. This framework allows us to identify optimal depth and width configurations, providing a unified explanation for fundamental DNN behaviors such as the "flat minima effect," "grokking," and double descent phenomena. Our analysis extends to networks with depths up to 100 layers.

How and what to learn:The modes of machine learning

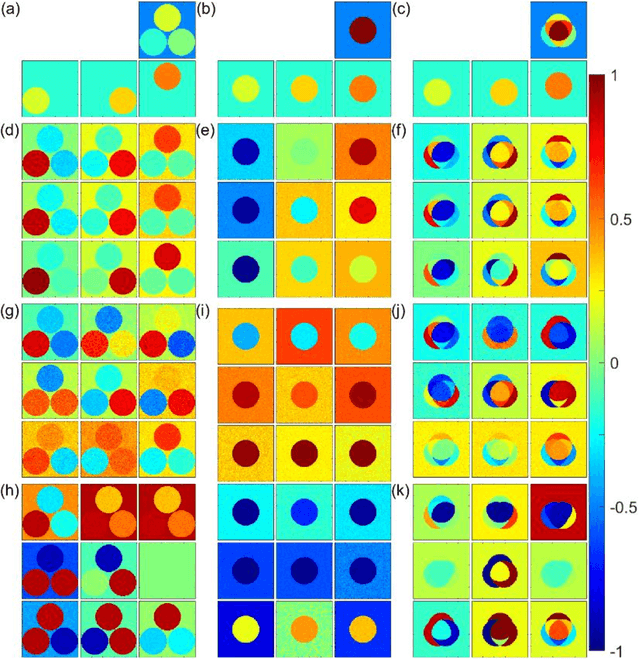
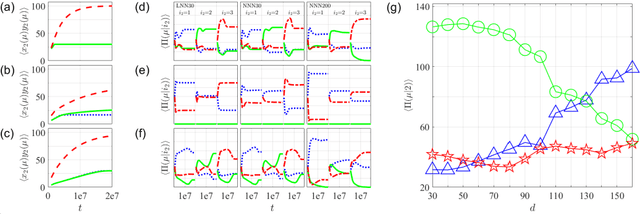
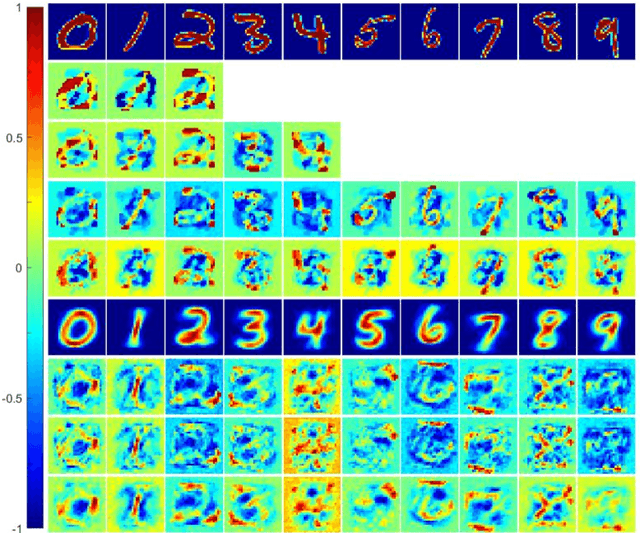
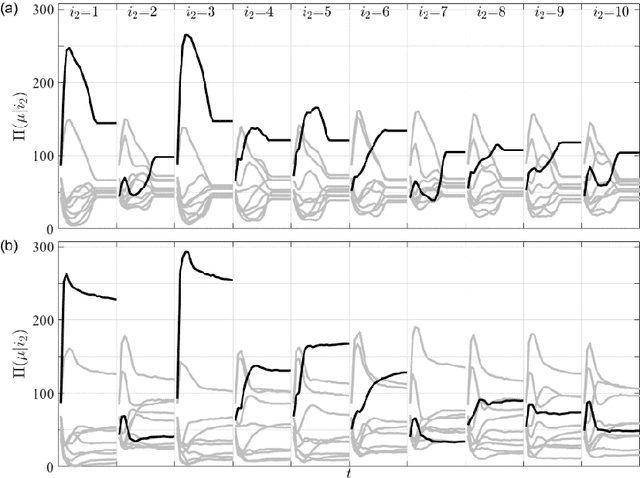
We proposal a new approach, namely the weight pathway analysis (WPA), to study the mechanism of multilayer neural networks. The weight pathways linking neurons longitudinally from input neurons to output neurons are considered as the basic units of a neural network. We decompose a neural network into a series of subnetworks of weight pathways, and establish characteristic maps for these subnetworks. The parameters of a characteristic map can be visualized, providing a longitudinal perspective of the network and making the neural network explainable. Using WPA, we discover that a neural network stores and utilizes information in a "holographic" way, that is, the network encodes all training samples in a coherent structure. An input vector interacts with this "holographic" structure to enhance or suppress each subnetwork which working together to produce the correct activities in the output neurons to recognize the input sample. Furthermore, with WPA, we reveal fundamental learning modes of a neural network: the linear learning mode and the nonlinear learning mode. The former extracts linearly separable features while the latter extracts linearly inseparable features. It is found that hidden-layer neurons self-organize into different classes in the later stages of the learning process. It is further discovered that the key strategy to improve the performance of a neural network is to control the ratio of the two learning modes to match that of the linear and the nonlinear features, and that increasing the width or the depth of a neural network helps this ratio controlling process. This provides theoretical ground for the practice of optimizing a neural network via increasing its width or its depth. The knowledge gained with WPA enables us to understand the fundamental questions such as what to learn, how to learn, and how can learn well.