A Latency-Aware Framework for Visuomotor Policy Learning on Industrial Robots

Industrial robots are increasingly deployed in contact-rich construction and manufacturing tasks that involve uncertainty and long-horizon execution. While learning-based visuomotor policies offer a promising alternative to open-loop control, their deployment on industrial platforms is challenged by a large observation-execution gap caused by sensing, inference, and control latency. This gap is significantly greater than on low-latency research robots due to high-level interfaces and slower closed-loop dynamics, making execution timing a critical system-level issue. This paper presents a latency-aware framework for deploying and evaluating visuomotor policies on industrial robotic arms under realistic timing constraints. The framework integrates calibrated multimodal sensing, temporally consistent synchronization, a unified communication pipeline, and a teleoperation interface for demonstration collection. Within this framework, we introduce a latency-aware execution strategy that schedules finite-horizon, policy-predicted action sequences based on temporal feasibility, enabling asynchronous inference and execution without modifying policy architectures or training. We evaluate the framework on a contact-rich industrial assembly task while systematically varying inference latency. Using identical policies and sensing pipelines, we compare latency-aware execution with blocking and naive asynchronous baselines. Results show that latency-aware execution maintains smooth motion, compliant contact behavior, and consistent task progression across a wide range of latencies while reducing idle time and avoiding instability observed in baseline methods. These findings highlight the importance of explicitly handling latency for reliable closed-loop deployment of visuomotor policies on industrial robots.

Learning the nonlinear dynamics of soft mechanical metamaterials with graph networks

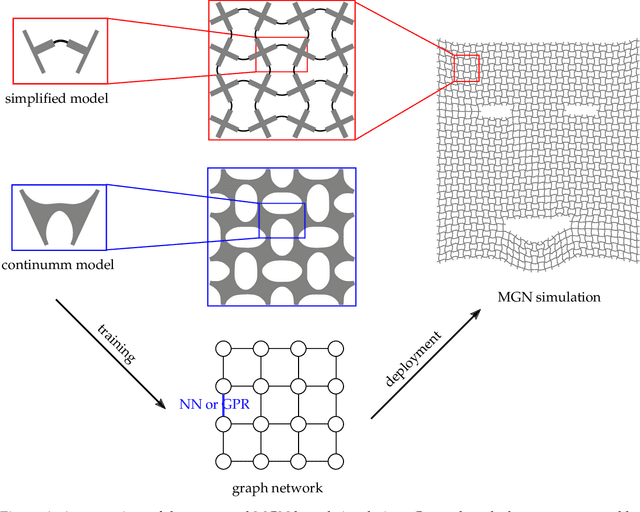
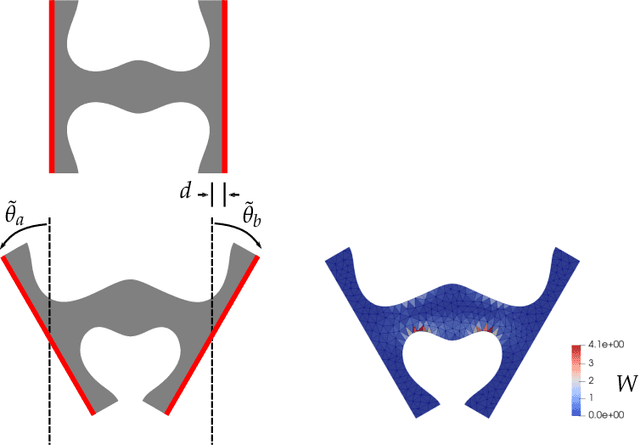
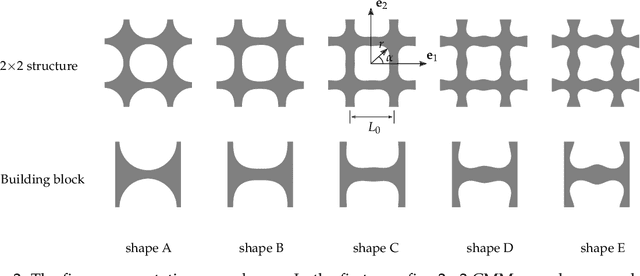
The dynamics of soft mechanical metamaterials provides opportunities for many exciting engineering applications. Previous studies often use discrete systems, composed of rigid elements and nonlinear springs, to model the nonlinear dynamic responses of the continuum metamaterials. Yet it remains a challenge to accurately construct such systems based on the geometry of the building blocks of the metamaterial. In this work, we propose a machine learning approach to address this challenge. A metamaterial graph network (MGN) is used to represent the discrete system, where the nodal features contain the positions and orientations the rigid elements, and the edge update functions describe the mechanics of the nonlinear springs. We use Gaussian process regression as the surrogate model to characterize the elastic energy of the nonlinear springs as a function of the relative positions and orientations of the connected rigid elements. The optimal model can be obtained by "learning" from the data generated via finite element calculation over the corresponding building block of the continuum metamaterial. Then, we deploy the optimal model to the network so that the dynamics of the metamaterial at the structural scale can be studied. We verify the accuracy of our machine learning approach against several representative numerical examples. In these examples, the proposed approach can significantly reduce the computational cost when compared to direct numerical simulation while reaching comparable accuracy. Moreover, defects and spatial inhomogeneities can be easily incorporated into our approach, which can be useful for the rational design of soft mechanical metamaterials.

Three Cooperative Robotic Fabrication Methods for the Scaffold-Free Construction of a Masonry Arch

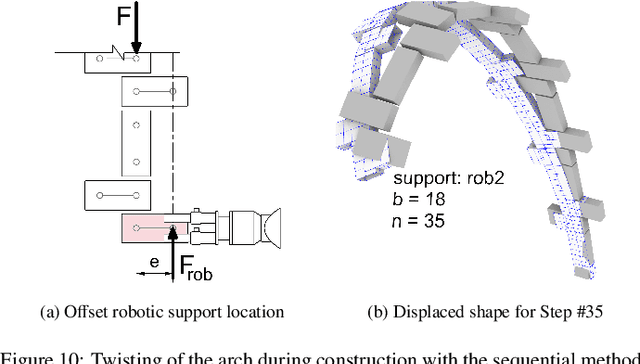
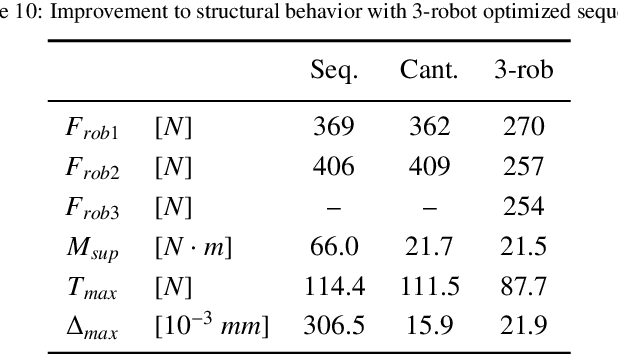
Geometrically complex masonry structures (e.g., arches, domes, vaults) are traditionally built with expensive scaffolding or falsework to provide stability during construction. The process of building such structures can potentially be improved through the use of multiple robots working together in a cooperative assembly framework. Here a robot is envisioned as both a placement and external support agent during fabrication - the unfinished structure is supported in such a way that scaffolding is not required. The goal of this paper is to present and validate the efficacy of three cooperative fabrication approaches using two or three robots, for the scaffold-free construction of a stable masonry arch from which a medium-span vault is built. A simplified numerical method to represent a masonry structure is first presented and validated to analyse systems composed of discrete volumetric elements. This method is then used to evaluate the effect of the three cooperative robotic fabrication strategies on the stability performance of the central arch. The sequential method and cantilever method, which utilize two robotic arms, are shown to be viable methods, but have challenges related to scalability and robustness. By adding a third robotic agent, it becomes possible to determine a structurally optimal fabrication sequence through a multi-objective optimization process. The optimized three robot method is shown to significantly improve the structural behavior over all fabrication steps. The modeling approaches presented in this paper are broadly formulated and widely applicable for the analysis of cooperative robotic fabrication sequences for the construction of discrete element structures across scales and materials.