Translation Of Telugu-Marathi and Vice-Versa using Rule Based Machine Translation

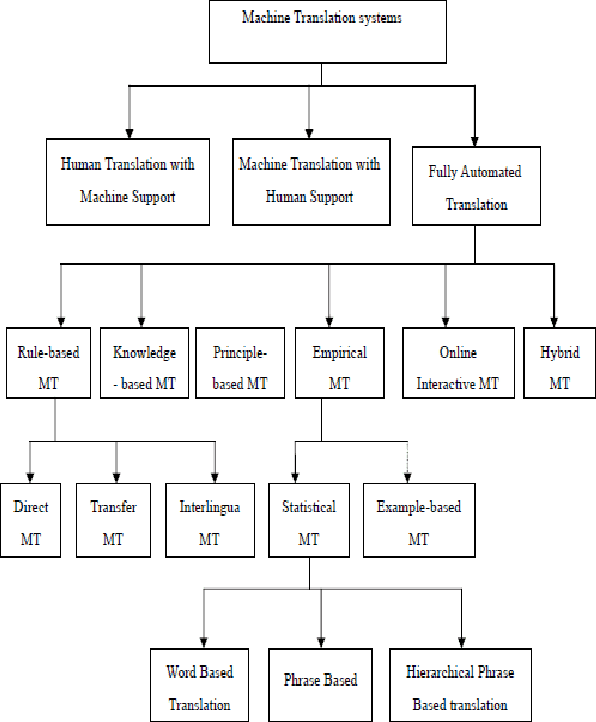
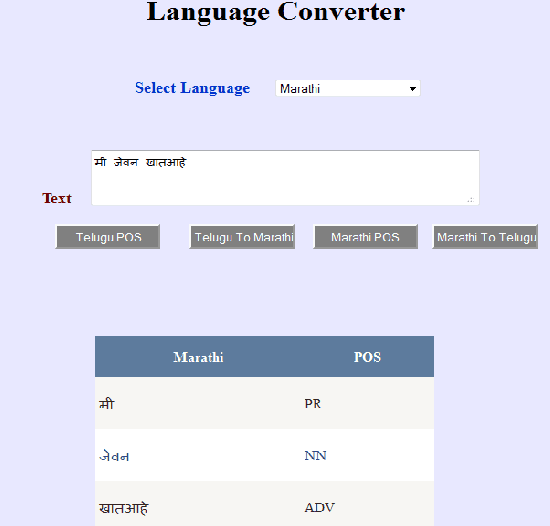
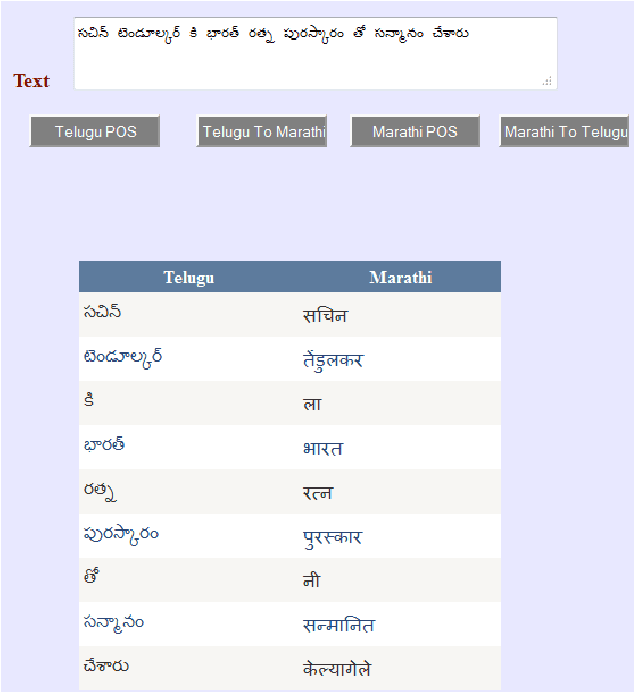
In todays digital world automated Machine Translation of one language to another has covered a long way to achieve different kinds of success stories. Whereas Babel Fish supports a good number of foreign languages and only Hindi from Indian languages, the Google Translator takes care of about 10 Indian languages. Though most of the Automated Machine Translation Systems are doing well but handling Indian languages needs a major care while handling the local proverbs/ idioms. Most of the Machine Translation system follows the direct translation approach while translating one Indian language to other. Our research at KMIT R&D Lab found that handling the local proverbs/idioms is not given enough attention by the earlier research work. This paper focuses on two of the majorly spoken Indian languages Marathi and Telugu, and translation between them. Handling proverbs and idioms of both the languages have been given a special care, and the research outcome shows a significant achievement in this direction.

Efficient State-Space Inference of Periodic Latent Force Models

Latent force models (LFM) are principled approaches to incorporating solutions to differential equations within non-parametric inference methods. Unfortunately, the development and application of LFMs can be inhibited by their computational cost, especially when closed-form solutions for the LFM are unavailable, as is the case in many real world problems where these latent forces exhibit periodic behaviour. Given this, we develop a new sparse representation of LFMs which considerably improves their computational efficiency, as well as broadening their applicability, in a principled way, to domains with periodic or near periodic latent forces. Our approach uses a linear basis model to approximate one generative model for each periodic force. We assume that the latent forces are generated from Gaussian process priors and develop a linear basis model which fully expresses these priors. We apply our approach to model the thermal dynamics of domestic buildings and show that it is effective at predicting day-ahead temperatures within the homes. We also apply our approach within queueing theory in which quasi-periodic arrival rates are modelled as latent forces. In both cases, we demonstrate that our approach can be implemented efficiently using state-space methods which encode the linear dynamic systems via LFMs. Further, we show that state estimates obtained using periodic latent force models can reduce the root mean squared error to 17% of that from non-periodic models and 27% of the nearest rival approach which is the resonator model.