Block Coordinate Descent for Neural Networks Provably Finds Global Minima

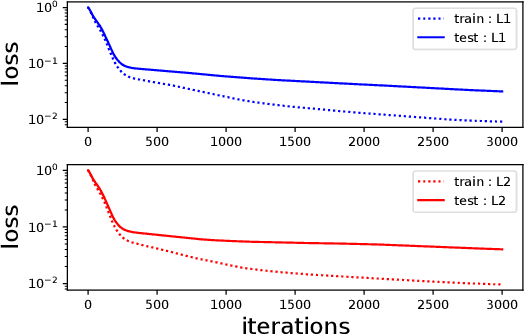
In this paper, we consider a block coordinate descent (BCD) algorithm for training deep neural networks and provide a new global convergence guarantee under strictly monotonically increasing activation functions. While existing works demonstrate convergence to stationary points for BCD in neural networks, our contribution is the first to prove convergence to global minima, ensuring arbitrarily small loss. We show that the loss with respect to the output layer decreases exponentially while the loss with respect to the hidden layers remains well-controlled. Additionally, we derive generalization bounds using the Rademacher complexity framework, demonstrating that BCD not only achieves strong optimization guarantees but also provides favorable generalization performance. Moreover, we propose a modified BCD algorithm with skip connections and non-negative projection, extending our convergence guarantees to ReLU activation, which are not strictly monotonic. Empirical experiments confirm our theoretical findings, showing that the BCD algorithm achieves a small loss for strictly monotonic and ReLU activations.

Diffusion Models are Minimax Optimal Distribution Estimators

While efficient distribution learning is no doubt behind the groundbreaking success of diffusion modeling, its theoretical guarantees are quite limited. In this paper, we provide the first rigorous analysis on approximation and generalization abilities of diffusion modeling for well-known function spaces. The highlight of this paper is that when the true density function belongs to the Besov space and the empirical score matching loss is properly minimized, the generated data distribution achieves the nearly minimax optimal estimation rates in the total variation distance and in the Wasserstein distance of order one. Furthermore, we extend our theory to demonstrate how diffusion models adapt to low-dimensional data distributions. We expect these results advance theoretical understandings of diffusion modeling and its ability to generate verisimilar outputs.

Excess Risk of Two-Layer ReLU Neural Networks in Teacher-Student Settings and its Superiority to Kernel Methods

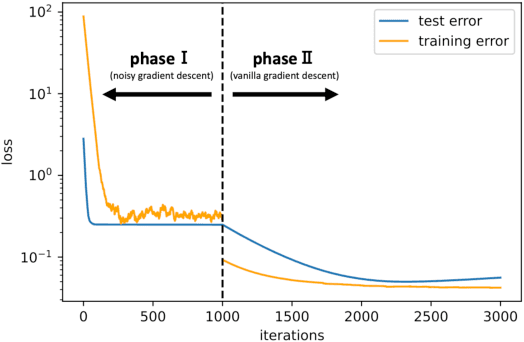
While deep learning has outperformed other methods for various tasks, theoretical frameworks that explain its reason have not been fully established. To address this issue, we investigate the excess risk of two-layer ReLU neural networks in a teacher-student regression model, in which a student network learns an unknown teacher network through its outputs. Especially, we consider the student network that has the same width as the teacher network and is trained in two phases: first by noisy gradient descent and then by the vanilla gradient descent. Our result shows that the student network provably reaches a near-global optimal solution and outperforms any kernel methods estimator (more generally, linear estimators), including neural tangent kernel approach, random feature model, and other kernel methods, in a sense of the minimax optimal rate. The key concept inducing this superiority is the non-convexity of the neural network models. Even though the loss landscape is highly non-convex, the student network adaptively learns the teacher neurons.

On Learnability via Gradient Method for Two-Layer ReLU Neural Networks in Teacher-Student Setting

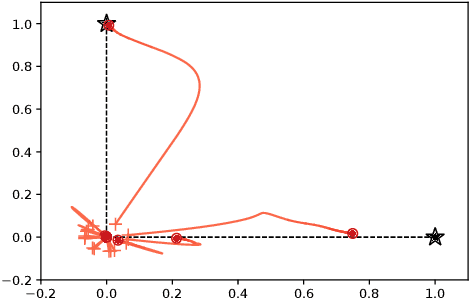
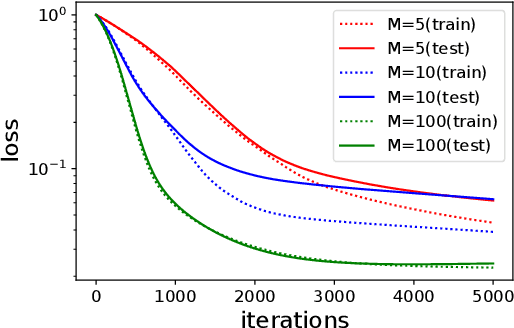
Deep learning empirically achieves high performance in many applications, but its training dynamics has not been fully understood theoretically. In this paper, we explore theoretical analysis on training two-layer ReLU neural networks in a teacher-student regression model, in which a student network learns an unknown teacher network through its outputs. We show that with a specific regularization and sufficient over-parameterization, the student network can identify the parameters of the teacher network with high probability via gradient descent with a norm dependent stepsize even though the objective function is highly non-convex. The key theoretical tool is the measure representation of the neural networks and a novel application of a dual certificate argument for sparse estimation on a measure space. We analyze the global minima and global convergence property in the measure space.

Benefit of deep learning with non-convex noisy gradient descent: Provable excess risk bound and superiority to kernel methods

Establishing a theoretical analysis that explains why deep learning can outperform shallow learning such as kernel methods is one of the biggest issues in the deep learning literature. Towards answering this question, we evaluate excess risk of a deep learning estimator trained by a noisy gradient descent with ridge regularization on a mildly overparameterized neural network, and discuss its superiority to a class of linear estimators that includes neural tangent kernel approach, random feature model, other kernel methods, $k$-NN estimator and so on. We consider a teacher-student regression model, and eventually show that any linear estimator can be outperformed by deep learning in a sense of the minimax optimal rate especially for a high dimension setting. The obtained excess bounds are so-called fast learning rate which is faster than $O(1/\sqrt{n})$ that is obtained by usual Rademacher complexity analysis. This discrepancy is induced by the non-convex geometry of the model and the noisy gradient descent used for neural network training provably reaches a near global optimal solution even though the loss landscape is highly non-convex. Although the noisy gradient descent does not employ any explicit or implicit sparsity inducing regularization, it shows a preferable generalization performance that dominates linear estimators.