Excess Risk of Two-Layer ReLU Neural Networks in Teacher-Student Settings and its Superiority to Kernel Methods
Paper and Code
Jun 06, 2022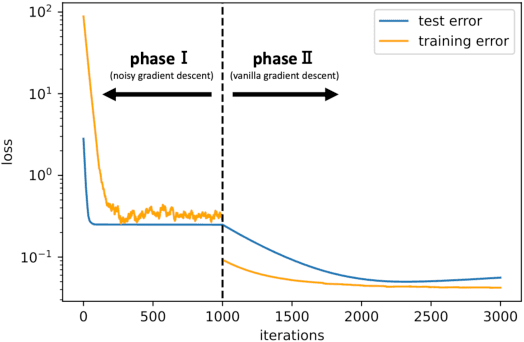
While deep learning has outperformed other methods for various tasks, theoretical frameworks that explain its reason have not been fully established. To address this issue, we investigate the excess risk of two-layer ReLU neural networks in a teacher-student regression model, in which a student network learns an unknown teacher network through its outputs. Especially, we consider the student network that has the same width as the teacher network and is trained in two phases: first by noisy gradient descent and then by the vanilla gradient descent. Our result shows that the student network provably reaches a near-global optimal solution and outperforms any kernel methods estimator (more generally, linear estimators), including neural tangent kernel approach, random feature model, and other kernel methods, in a sense of the minimax optimal rate. The key concept inducing this superiority is the non-convexity of the neural network models. Even though the loss landscape is highly non-convex, the student network adaptively learns the teacher neurons.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge