MathCAMPS: Fine-grained Synthesis of Mathematical Problems From Human Curricula

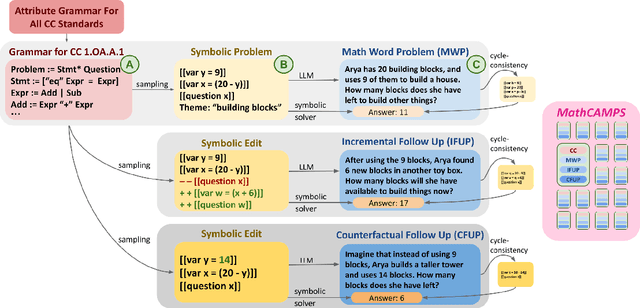
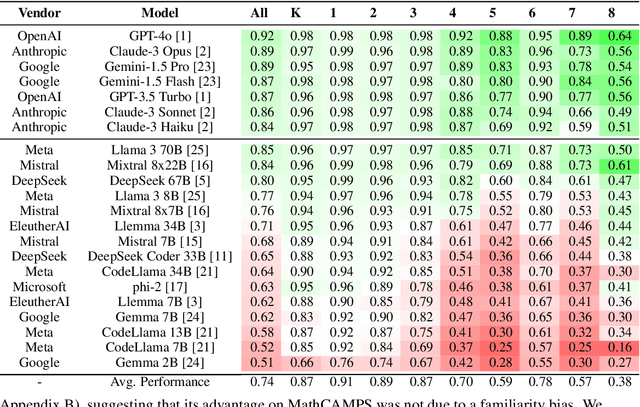
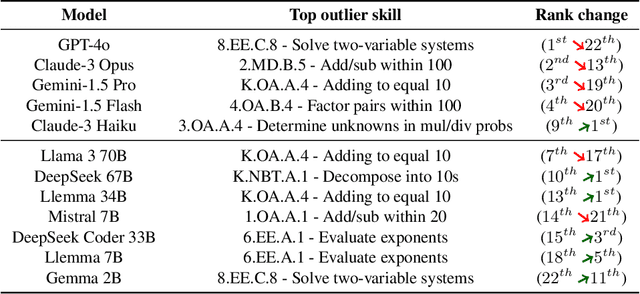
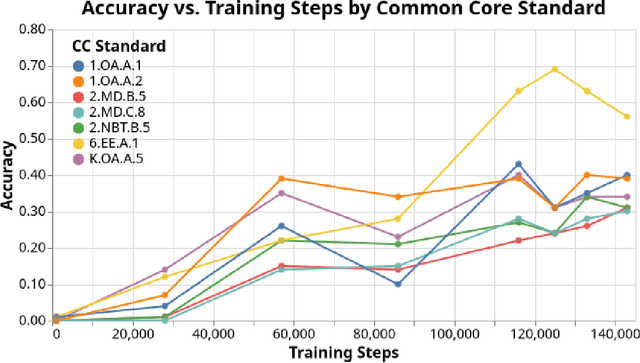
Mathematical problem solving is an important skill for Large Language Models (LLMs), both as an important capability and a proxy for a range of reasoning abilities. Existing benchmarks probe a diverse set of skills, but they yield aggregate accuracy metrics, obscuring specific abilities or weaknesses. Furthermore, they are difficult to extend with new problems, risking data contamination over time. To address these challenges, we propose MathCAMPS: a method to synthesize high-quality mathematical problems at scale, grounded on 44 fine-grained "standards" from the Mathematics Common Core (CC) Standard for K-8 grades. We encode each standard in a formal grammar, allowing us to sample diverse symbolic problems and their answers. We then use LLMs to realize the symbolic problems into word problems. We propose a cycle-consistency method for validating problem faithfulness. Finally, we derive follow-up questions from symbolic structures and convert them into follow-up word problems - a novel task of mathematical dialogue that probes for robustness in understanding. Experiments on 23 LLMs show surprising failures even in the strongest models (in particular when asked simple follow-up questions). Moreover, we evaluate training checkpoints of Pythia 12B on MathCAMPS, allowing us to analyze when particular mathematical skills develop during its training. Our framework enables the community to reproduce and extend our pipeline for a fraction of the typical cost of building new high-quality datasets.

An Evaluation Benchmark for Autoformalization in Lean4

Large Language Models (LLMs) hold the potential to revolutionize autoformalization. The introduction of Lean4, a mathematical programming language, presents an unprecedented opportunity to rigorously assess the autoformalization capabilities of LLMs. This paper introduces a novel evaluation benchmark designed for Lean4, applying it to test the abilities of state-of-the-art LLMs, including GPT-3.5, GPT-4, and Gemini Pro. Our comprehensive analysis reveals that, despite recent advancements, these LLMs still exhibit limitations in autoformalization, particularly in more complex areas of mathematics. These findings underscore the need for further development in LLMs to fully harness their potential in scientific research and development. This study not only benchmarks current LLM capabilities but also sets the stage for future enhancements in autoformalization.