Select-Mosaic: Data Augmentation Method for Dense Small Object Scenes

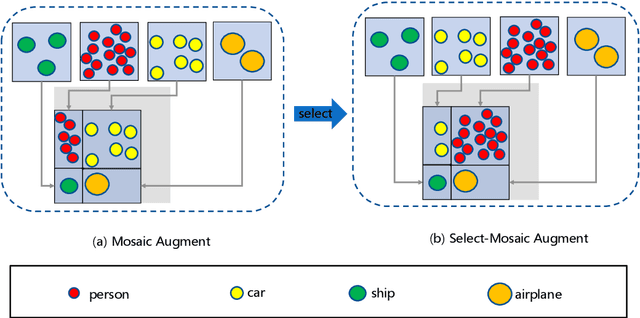
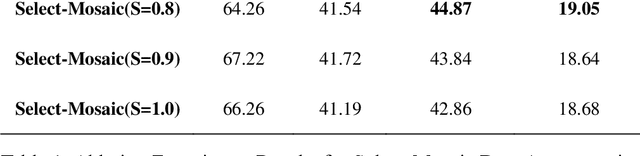
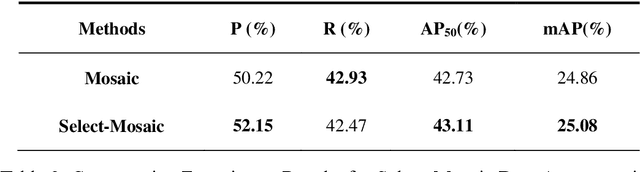
Data augmentation refers to the process of applying a series of transformations or expansions to original data to generate new samples, thereby increasing the diversity and quantity of the data, effectively improving the performance and robustness of models. As a common data augmentation method, Mosaic data augmentation technique stitches multiple images together to increase the diversity and complexity of training data, thereby reducing the risk of overfitting. Although Mosaic data augmentation achieves excellent results in general detection tasks by stitching images together, it still has certain limitations for specific detection tasks. This paper addresses the challenge of detecting a large number of densely distributed small objects in aerial images by proposing the Select-Mosaic data augmentation method, which is improved with a fine-grained region selection strategy. The improved Select-Mosaic method demonstrates superior performance in handling dense small object detection tasks, significantly enhancing the accuracy and stability of detection models. Code is available at https://github.com/malagoutou/Select-Mosaic.

Focaler-IoU: More Focused Intersection over Union Loss

Bounding box regression plays a crucial role in the field of object detection, and the positioning accuracy of object detection largely depends on the loss function of bounding box regression. Existing researchs improve regression performance by utilizing the geometric relationship between bounding boxes, while ignoring the impact of difficult and easy sample distribution on bounding box regression. In this article, we analyzed the impact of difficult and easy sample distribution on regression results, and then proposed Focaler-IoU, which can improve detector performance in different detection tasks by focusing on different regression samples. Finally, comparative experiments were conducted using existing advanced detectors and regression methods for different detection tasks, and the detection performance was further improved by using the method proposed in this paper.Code is available at \url{https://github.com/malagoutou/Focaler-IoU}.

Shape-IoU: More Accurate Metric considering Bounding Box Shape and Scale

As an important component of the detector localization branch, bounding box regression loss plays a significant role in object detection tasks. The existing bounding box regression methods usually consider the geometric relationship between the GT box and the predicted box, and calculate the loss by using the relative position and shape of the bounding boxes, while ignoring the influence of inherent properties such as the shape and scale of the bounding boxes on bounding box regression. In order to make up for the shortcomings of existing research, this article proposes a bounding box regression method that focuses on the shape and scale of the bounding box itself. Firstly, we analyzed the regression characteristics of the bounding boxes and found that the shape and scale factors of the bounding boxes themselves will have an impact on the regression results. Based on the above conclusions, we propose the Shape IoU method, which can calculate the loss by focusing on the shape and scale of the bounding box itself, thereby making the bounding box regression more accurate. Finally, we validated our method through a large number of comparative experiments, which showed that our method can effectively improve detection performance and outperform existing methods, achieving state-of-the-art performance in different detection tasks.Code is available at https://github.com/malagoutou/Shape-IoU

Inner-IoU: More Effective Intersection over Union Loss with Auxiliary Bounding Box

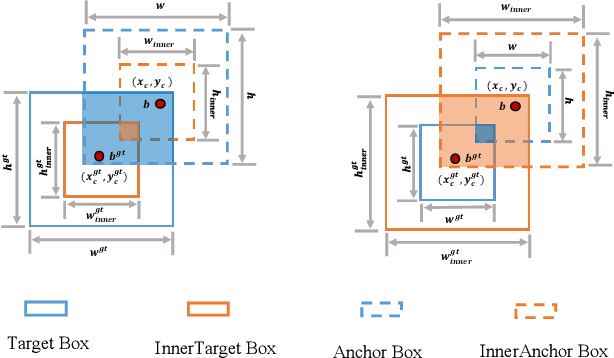
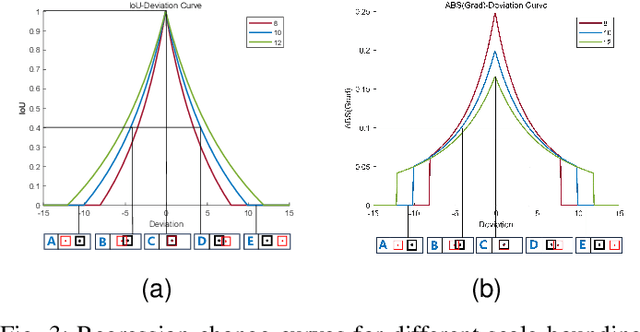
With the rapid development of detectors, Bounding Box Regression (BBR) loss function has constantly updated and optimized. However, the existing IoU-based BBR still focus on accelerating convergence by adding new loss terms, ignoring the limitations of IoU loss term itself. Although theoretically IoU loss can effectively describe the state of bounding box regression,in practical applications, it cannot adjust itself according to different detectors and detection tasks, and does not have strong generalization. Based on the above, we first analyzed the BBR model and concluded that distinguishing different regression samples and using different scales of auxiliary bounding boxes to calculate losses can effectively accelerate the bounding box regression process. For high IoU samples, using smaller auxiliary bounding boxes to calculate losses can accelerate convergence, while larger auxiliary bounding boxes are suitable for low IoU samples. Then, we propose Inner-IoU loss, which calculates IoU loss through auxiliary bounding boxes. For different datasets and detectors, we introduce a scaling factor ratio to control the scale size of the auxiliary bounding boxes for calculating losses. Finally, integrate Inner-IoU into the existing IoU-based loss functions for simulation and comparative experiments. The experiment result demonstrate a further enhancement in detection performance with the utilization of the method proposed in this paper, verifying the effectiveness and generalization ability of Inner-IoU loss. Code is available at https://github.com/malagoutou/Inner-IoU.