Shota Okumura
Quick sensitivity analysis for incremental data modification and its application to leave-one-out CV in linear classification problems
Apr 11, 2015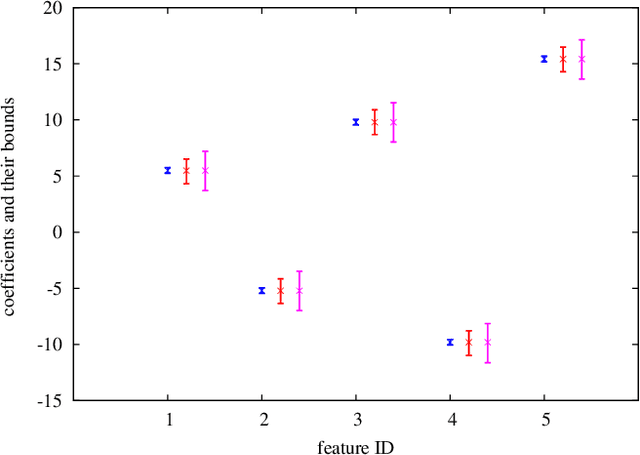

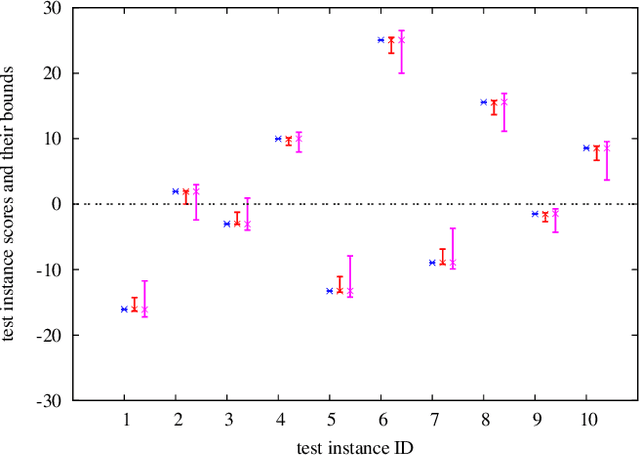

Abstract:We introduce a novel sensitivity analysis framework for large scale classification problems that can be used when a small number of instances are incrementally added or removed. For quickly updating the classifier in such a situation, incremental learning algorithms have been intensively studied in the literature. Although they are much more efficient than solving the optimization problem from scratch, their computational complexity yet depends on the entire training set size. It means that, if the original training set is large, completely solving an incremental learning problem might be still rather expensive. To circumvent this computational issue, we propose a novel framework that allows us to make an inference about the updated classifier without actually re-optimizing it. Specifically, the proposed framework can quickly provide a lower and an upper bounds of a quantity on the unknown updated classifier. The main advantage of the proposed framework is that the computational cost of computing these bounds depends only on the number of updated instances. This property is quite advantageous in a typical sensitivity analysis task where only a small number of instances are updated. In this paper we demonstrate that the proposed framework is applicable to various practical sensitivity analysis tasks, and the bounds provided by the framework are often sufficiently tight for making desired inferences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge