Interval-valued fuzzy soft $β$-covering approximation spaces

The concept of interval-valued fuzzy soft $\beta$-covering approximation spaces (IFS$\beta$CASs) is introduced to combine the theories of soft sets, rough sets and interval-valued fuzzy sets, and some fundamental propositions concerning interval-valued fuzzy soft $\beta$-neighborhoods and soft $\beta$-neighborhoods of IFS$\beta$CASs are explored. And then four kinds of interval-valued fuzzy soft $\beta$-coverings based fuzzy rough sets are researched. Finally, the relationships of four kinds of interval-valued fuzzy soft $\beta$-coverings based fuzzy rough sets are investigated.

Foundational propositions of hesitant fuzzy soft $β$-covering approximation spaces

Soft set theory serves as a mathematical framework for handling uncertain information, and hesitant fuzzy sets find extensive application in scenarios involving uncertainty and hesitation. Hesitant fuzzy sets exhibit diverse membership degrees, giving rise to various forms of inclusion relationships among them. This article introduces the notions of hesitant fuzzy soft $\beta$-coverings and hesitant fuzzy soft $\beta$-neighborhoods, which are formulated based on distinct forms of inclusion relationships among hesitancy fuzzy sets. Subsequently, several associated properties are investigated. Additionally, specific variations of hesitant fuzzy soft $\beta$-coverings are introduced by incorporating hesitant fuzzy rough sets, followed by an exploration of properties pertaining to hesitant fuzzy soft $\beta$-covering approximation spaces.

Foundational propositions of hesitant fuzzy sets and parameter reductions of hesitant fuzzy information systems

Hesitant fuzzy sets are widely used in the instances of uncertainty and hesitation. The inclusion relationship is an important and foundational definition for sets. Hesitant fuzzy set, as a kind of set, needs explicit definition of inclusion relationship. Base on the hesitant fuzzy membership degree of discrete form, several kinds of inclusion relationships for hesitant fuzzy sets are proposed. And then some foundational propositions of hesitant fuzzy sets and the families of hesitant fuzzy sets are presented. Finally, some foundational propositions of hesitant fuzzy information systems with respect to parameter reductions are put forward, and an example and an algorithm are given to illustrate the processes of parameter reductions.

A self-adaptive and robust fission clustering algorithm via heat diffusion and maximal turning angle

Cluster analysis, which focuses on the grouping and categorization of similar elements, is widely used in various fields of research. A novel and fast clustering algorithm, fission clustering algorithm, is proposed in recent year. In this article, we propose a robust fission clustering (RFC) algorithm and a self-adaptive noise identification method. The RFC and the self-adaptive noise identification method are combine to propose a self-adaptive robust fission clustering (SARFC) algorithm. Several frequently-used datasets were applied to test the performance of the proposed clustering approach and to compare the results with those of other algorithms. The comprehensive comparisons indicate that the proposed method has advantages over other common methods.

Self-adaption grey DBSCAN clustering

Clustering analysis, a classical issue in data mining, is widely used in various research areas. This article aims at proposing a self-adaption grey DBSCAN clustering (SAG-DBSCAN) algorithm. First, the grey relational matrix is used to obtain the grey local density indicator, and then this indicator is applied to make self-adapting noise identification for obtaining a dense subset of clustering dataset, finally, the DBSCAN which automatically selects parameters is utilized to cluster the dense subset. Several frequently-used datasets were used to demonstrate the performance and effectiveness of the proposed clustering algorithm and to compare the results with those of other state-of-the-art algorithms. The comprehensive comparisons indicate that our method has advantages over other compared methods.

Clustering by the way of atomic fission

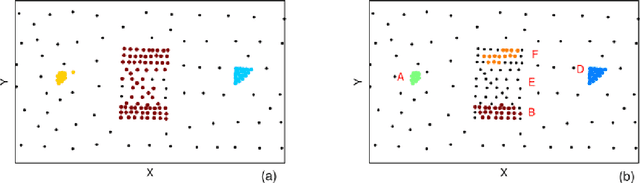
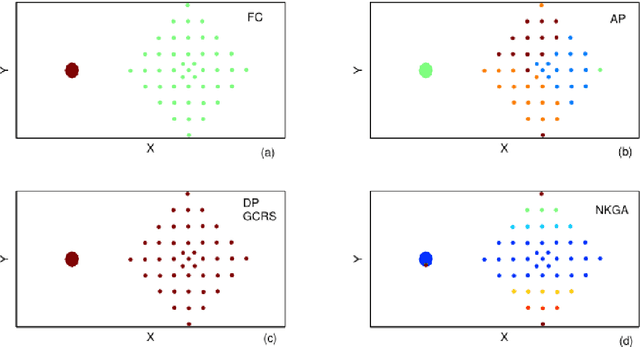
Cluster analysis which focuses on the grouping and categorization of similar elements is widely used in various fields of research. Inspired by the phenomenon of atomic fission, a novel density-based clustering algorithm is proposed in this paper, called fission clustering (FC). It focuses on mining the dense families of a dataset and utilizes the information of the distance matrix to fissure clustering dataset into subsets. When we face the dataset which has a few points surround the dense families of clusters, K-nearest neighbors local density indicator is applied to distinguish and remove the points of sparse areas so as to obtain a dense subset that is constituted by the dense families of clusters. A number of frequently-used datasets were used to test the performance of this clustering approach, and to compare the results with those of algorithms. The proposed algorithm is found to outperform other algorithms in speed and accuracy.