Anchor Data Augmentation

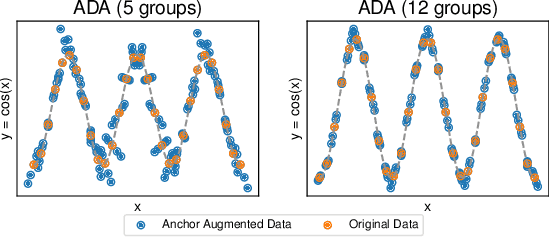
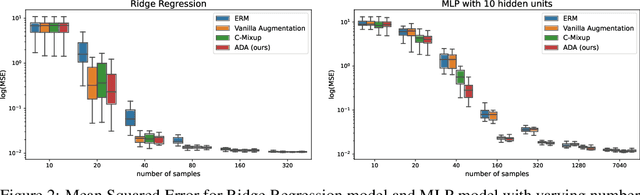
We propose a novel algorithm for data augmentation in nonlinear over-parametrized regression. Our data augmentation algorithm borrows from the literature on causality and extends the recently proposed Anchor regression (AR) method for data augmentation, which is in contrast to the current state-of-the-art domain-agnostic solutions that rely on the Mixup literature. Our Anchor Data Augmentation (ADA) uses several replicas of the modified samples in AR to provide more training examples, leading to more robust regression predictions. We apply ADA to linear and nonlinear regression problems using neural networks. ADA is competitive with state-of-the-art C-Mixup solutions.

Adaptive Annealed Importance Sampling with Constant Rate Progress

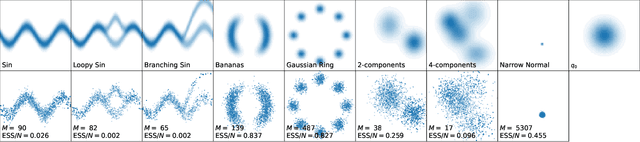
Annealed Importance Sampling (AIS) synthesizes weighted samples from an intractable distribution given its unnormalized density function. This algorithm relies on a sequence of interpolating distributions bridging the target to an initial tractable distribution such as the well-known geometric mean path of unnormalized distributions which is assumed to be suboptimal in general. In this paper, we prove that the geometric annealing corresponds to the distribution path that minimizes the KL divergence between the current particle distribution and the desired target when the feasible change in the particle distribution is constrained. Following this observation, we derive the constant rate discretization schedule for this annealing sequence, which adjusts the schedule to the difficulty of moving samples between the initial and the target distributions. We further extend our results to $f$-divergences and present the respective dynamics of annealing sequences based on which we propose the Constant Rate AIS (CR-AIS) algorithm and its efficient implementation for $\alpha$-divergences. We empirically show that CR-AIS performs well on multiple benchmark distributions while avoiding the computationally expensive tuning loop in existing Adaptive AIS.

Optimization of Annealed Importance Sampling Hyperparameters

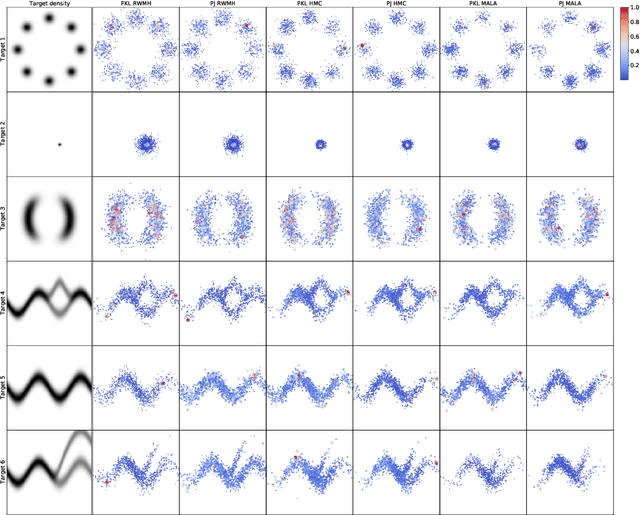
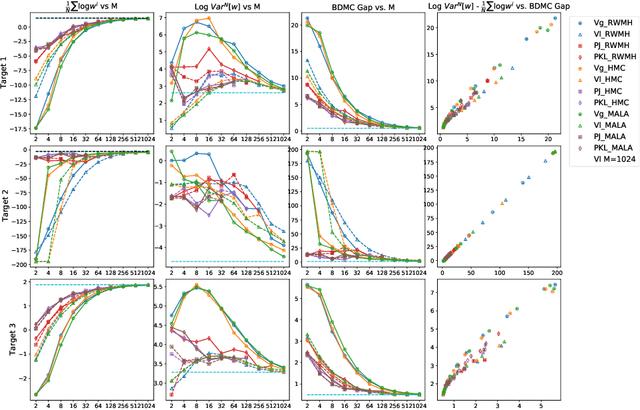
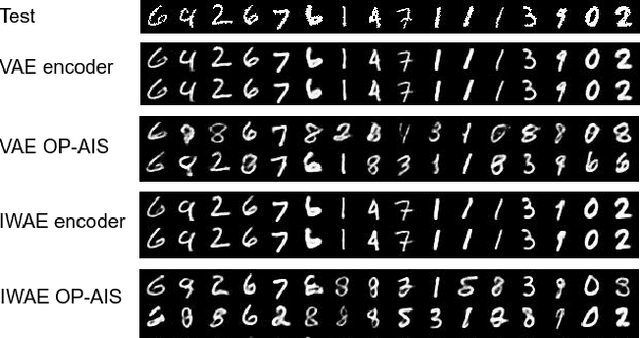
Annealed Importance Sampling (AIS) is a popular algorithm used to estimates the intractable marginal likelihood of deep generative models. Although AIS is guaranteed to provide unbiased estimate for any set of hyperparameters, the common implementations rely on simple heuristics such as the geometric average bridging distributions between initial and the target distribution which affect the estimation performance when the computation budget is limited. In order to reduce the number of sampling iterations, we present a parameteric AIS process with flexible intermediary distributions defined by a residual density with respect to the geometric mean path. Our method allows parameter sharing between annealing distributions, the use of fix linear schedule for discretization and amortization of hyperparameter selection in latent variable models. We assess the performance of Optimized-Path AIS for marginal likelihood estimation of deep generative models and compare it to compare it to more computationally intensive AIS.