Optimization of Annealed Importance Sampling Hyperparameters
Paper and Code
Oct 08, 2022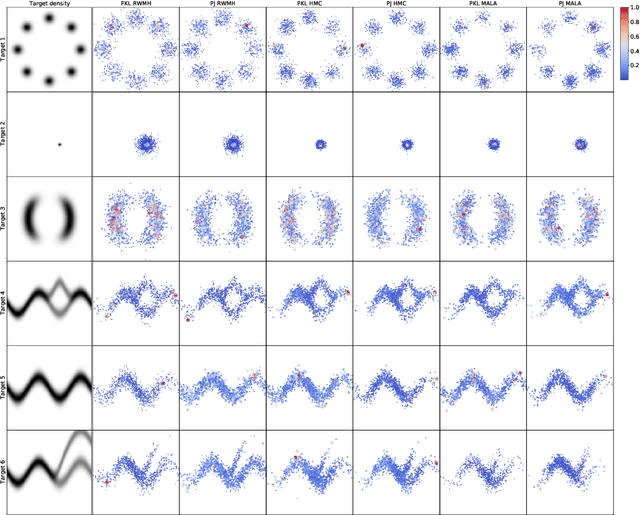

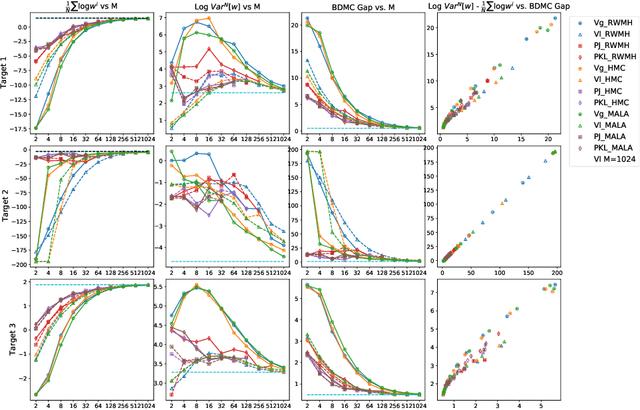
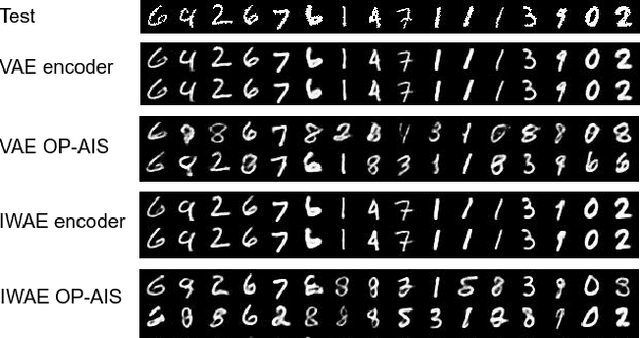
Annealed Importance Sampling (AIS) is a popular algorithm used to estimates the intractable marginal likelihood of deep generative models. Although AIS is guaranteed to provide unbiased estimate for any set of hyperparameters, the common implementations rely on simple heuristics such as the geometric average bridging distributions between initial and the target distribution which affect the estimation performance when the computation budget is limited. In order to reduce the number of sampling iterations, we present a parameteric AIS process with flexible intermediary distributions defined by a residual density with respect to the geometric mean path. Our method allows parameter sharing between annealing distributions, the use of fix linear schedule for discretization and amortization of hyperparameter selection in latent variable models. We assess the performance of Optimized-Path AIS for marginal likelihood estimation of deep generative models and compare it to compare it to more computationally intensive AIS.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge