Magnetohydrodynamics with Physics Informed Neural Operators

We present the first application of physics informed neural operators, which use tensor Fourier neural operators as their backbone, to model 2D incompressible magnetohydrodynamics simulations. Our results indicate that physics informed AI can accurately model the physics of magnetohydrodynamics simulations that describe laminar flows with Reynolds numbers $Re\leq250$. We also quantify the applicability of our AI surrogates for turbulent flows, and explore how magnetohydrodynamics simulations and AI surrogates store magnetic and kinetic energy across wavenumbers. Based on these studies, we propose a variety of approaches to create AI surrogates that provide a computationally efficient and high fidelity description of magnetohydrodynamics simulations for a broad range of Reynolds numbers. Neural operators and scientific software to produce simulation data to train, validate and test our physics informed neural operators are released with this manuscript.

Applications of physics informed neural operators

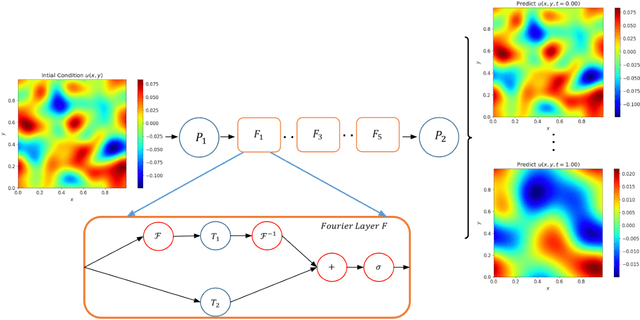
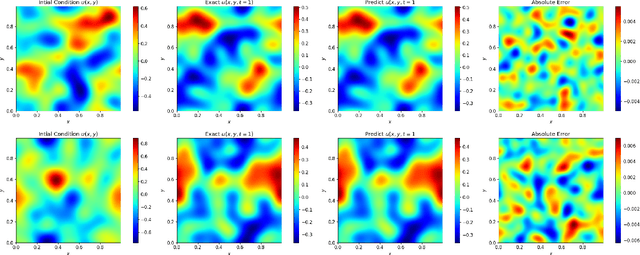
We present an end-to-end framework to learn partial differential equations that brings together initial data production, selection of boundary conditions, and the use of physics-informed neural operators to solve partial differential equations that are ubiquitous in the study and modeling of physics phenomena. We first demonstrate that our methods reproduce the accuracy and performance of other neural operators published elsewhere in the literature to learn the 1D wave equation and the 1D Burgers equation. Thereafter, we apply our physics-informed neural operators to learn new types of equations, including the 2D Burgers equation in the scalar, inviscid and vector types. Finally, we show that our approach is also applicable to learn the physics of the 2D linear and nonlinear shallow water equations, which involve three coupled partial differential equations. We release our artificial intelligence surrogates and scientific software to produce initial data and boundary conditions to study a broad range of physically motivated scenarios. We provide the source code, an interactive website to visualize the predictions of our physics informed neural operators, and a tutorial for their use at the Data and Learning Hub for Science.