Applications of physics informed neural operators
Paper and Code
Mar 23, 2022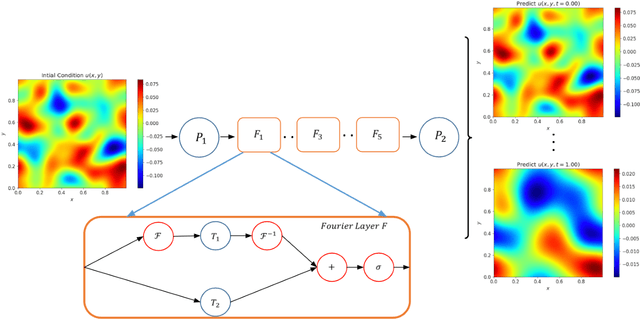

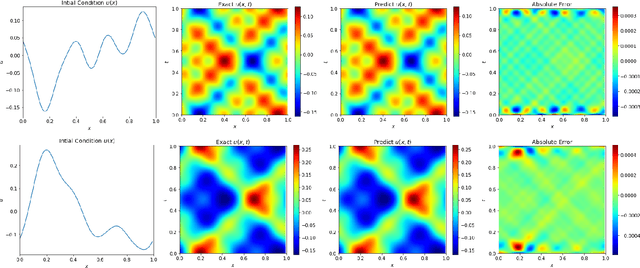
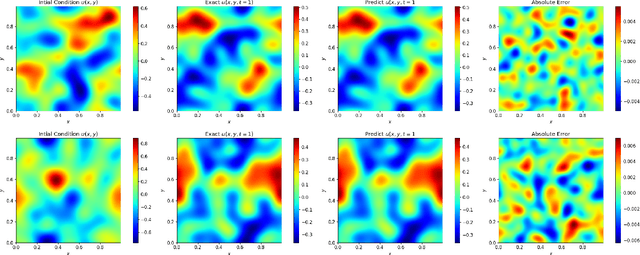
We present an end-to-end framework to learn partial differential equations that brings together initial data production, selection of boundary conditions, and the use of physics-informed neural operators to solve partial differential equations that are ubiquitous in the study and modeling of physics phenomena. We first demonstrate that our methods reproduce the accuracy and performance of other neural operators published elsewhere in the literature to learn the 1D wave equation and the 1D Burgers equation. Thereafter, we apply our physics-informed neural operators to learn new types of equations, including the 2D Burgers equation in the scalar, inviscid and vector types. Finally, we show that our approach is also applicable to learn the physics of the 2D linear and nonlinear shallow water equations, which involve three coupled partial differential equations. We release our artificial intelligence surrogates and scientific software to produce initial data and boundary conditions to study a broad range of physically motivated scenarios. We provide the source code, an interactive website to visualize the predictions of our physics informed neural operators, and a tutorial for their use at the Data and Learning Hub for Science.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge