Simultaneous Training of First- and Second-Order Optimizers in Population-Based Reinforcement Learning

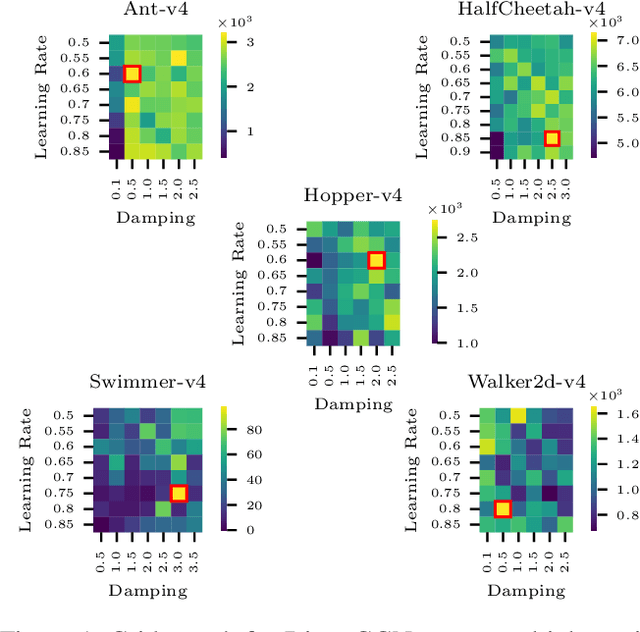
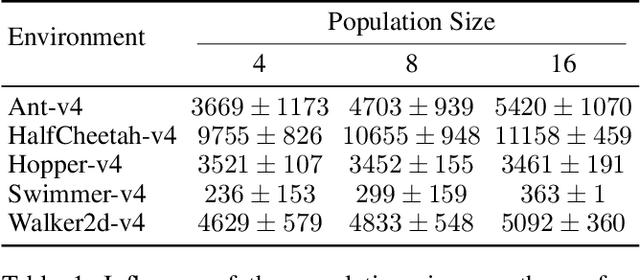
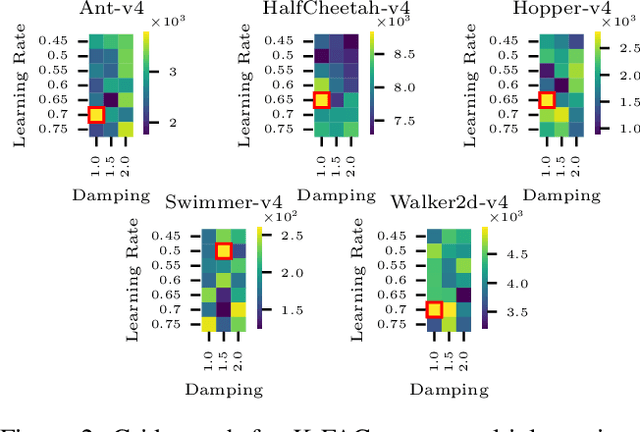
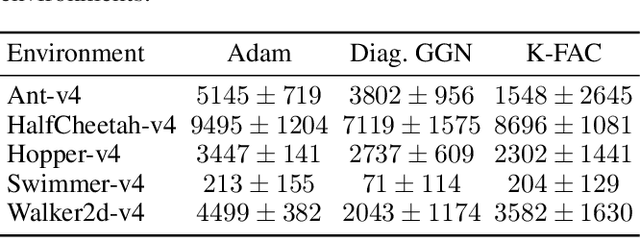
The tuning of hyperparameters in reinforcement learning (RL) is critical, as these parameters significantly impact an agent's performance and learning efficiency. Dynamic adjustment of hyperparameters during the training process can significantly enhance both the performance and stability of learning. Population-based training (PBT) provides a method to achieve this by continuously tuning hyperparameters throughout the training. This ongoing adjustment enables models to adapt to different learning stages, resulting in faster convergence and overall improved performance. In this paper, we propose an enhancement to PBT by simultaneously utilizing both first- and second-order optimizers within a single population. We conducted a series of experiments using the TD3 algorithm across various MuJoCo environments. Our results, for the first time, empirically demonstrate the potential of incorporating second-order optimizers within PBT-based RL. Specifically, the combination of the K-FAC optimizer with Adam led to up to a 10% improvement in overall performance compared to PBT using only Adam. Additionally, in environments where Adam occasionally fails, such as the Swimmer environment, the mixed population with K-FAC exhibited more reliable learning outcomes, offering a significant advantage in training stability without a substantial increase in computational time.

Efficient LSTM Training with Eligibility Traces

Training recurrent neural networks is predominantly achieved via backpropagation through time (BPTT). However, this algorithm is not an optimal solution from both a biological and computational perspective. A more efficient and biologically plausible alternative for BPTT is e-prop. We investigate the applicability of e-prop to long short-term memorys (LSTMs), for both supervised and reinforcement learning (RL) tasks. We show that e-prop is a suitable optimization algorithm for LSTMs by comparing it to BPTT on two benchmarks for supervised learning. This proves that e-prop can achieve learning even for problems with long sequences of several hundred timesteps. We introduce extensions that improve the performance of e-prop, which can partially be applied to other network architectures. With the help of these extensions we show that, under certain conditions, e-prop can outperform BPTT for one of the two benchmarks for supervised learning. Finally, we deliver a proof of concept for the integration of e-prop to RL in the domain of deep recurrent Q-learning.