Alignment Scores: Robust Metrics for Multiview Pose Accuracy Evaluation

We propose three novel metrics for evaluating the accuracy of a set of estimated camera poses given the ground truth: Translation Alignment Score (TAS), Rotation Alignment Score (RAS), and Pose Alignment Score (PAS). The TAS evaluates the translation accuracy independently of the rotations, and the RAS evaluates the rotation accuracy independently of the translations. The PAS is the average of the two scores, evaluating the combined accuracy of both translations and rotations. The TAS is computed in four steps: (1) Find the upper quartile of the closest-pair-distances, $d$. (2) Align the estimated trajectory to the ground truth using a robust registration method. (3) Collect all distance errors and obtain the cumulative frequencies for multiple thresholds ranging from $0.01d$ to $d$ with a resolution $0.01d$. (4) Add up these cumulative frequencies and normalize them such that the theoretical maximum is 1. The TAS has practical advantages over the existing metrics in that (1) it is robust to outliers and collinear motion, and (2) there is no need to adjust parameters on different datasets. The RAS is computed in a similar manner to the TAS and is also shown to be more robust against outliers than the existing rotation metrics. We verify our claims through extensive simulations and provide in-depth discussion of the strengths and weaknesses of the proposed metrics.

PCR-99: A Practical Method for Point Cloud Registration with 99% Outliers

We propose a robust method for point cloud registration that can handle both unknown scales and extreme outlier ratios. Our method, dubbed PCR-99, uses a deterministic 3-point sampling approach with two novel mechanisms that significantly boost the speed: (1) an improved ordering of the samples based on pairwise scale consistency, prioritizing the point correspondences that are more likely to be inliers, and (2) an efficient outlier rejection scheme based on triplet scale consistency, prescreening bad samples and reducing the number of hypotheses to be tested. Our evaluation shows that, up to 98% outlier ratio, the proposed method achieves comparable performance to the state of the art. At 99% outlier ratio, however, it outperforms the state of the art for both known-scale and unknown-scale problems. Especially for the latter, we observe a clear superiority in terms of robustness and speed.

Robust Single Rotation Averaging Revisited

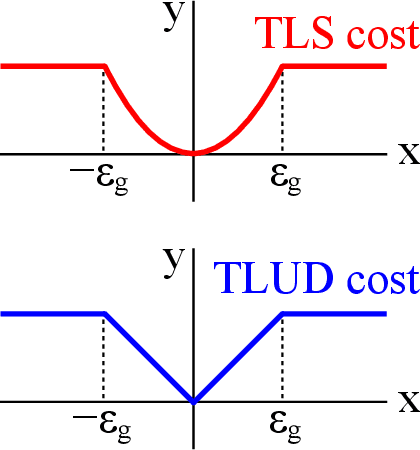
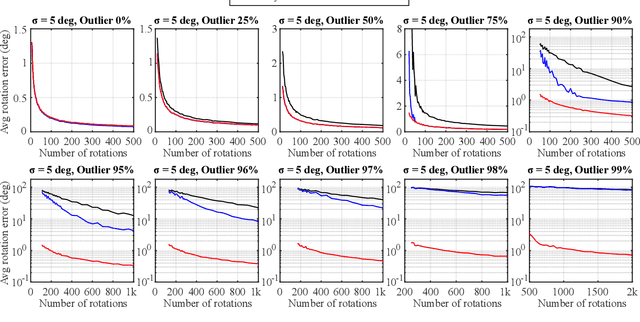
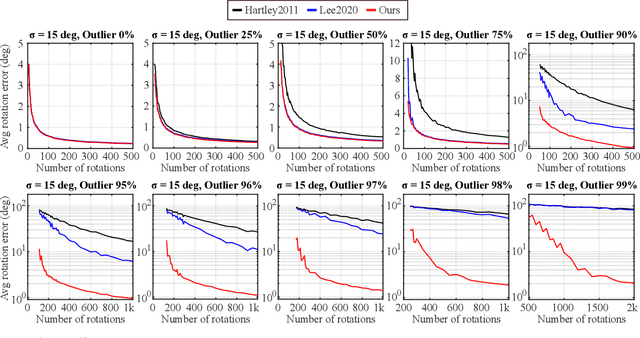
In this work, we propose a novel method for robust single rotation averaging that can efficiently handle an extremely large fraction of outliers. Our approach is to minimize the total truncated least unsquared deviations (TLUD) cost of geodesic distances. The proposed algorithm consists of three steps: First, we consider each input rotation as a potential initial solution and choose the one that yields the least sum of truncated chordal deviations. Next, we obtain the inlier set using the initial solution and compute its chordal $L_2$-mean. Finally, starting from this estimate, we iteratively compute the geodesic $L_1$-mean of the inliers using the Weiszfeld algorithm on $SO(3)$. An extensive evaluation shows that our method is robust against up to 99% outliers given a sufficient number of accurate inliers, outperforming the current state of the art.

What's Wrong with the Absolute Trajectory Error?

One of the main limitations of the commonly used Absolute Trajectory Error (ATE) is that it is highly sensitive to outliers. As a result, in the presence of just a few outliers, it often fails to reflect the varying accuracy as the inlier trajectory error or the number of outliers varies. In this work, we propose an alternative error metric for evaluating the accuracy of the reconstructed camera trajectory. Our metric, named Discernible Trajectory Error (DTE), is computed in four steps: (1) Shift the ground-truth and estimated trajectories such that both of their geometric medians are located at the origin. (2) Rotate the estimated trajectory such that it minimizes the sum of geodesic distances between the corresponding camera orientations. (3) Scale the estimated trajectory such that the median distance of the cameras to their geometric median is the same as that of the ground truth. (4) Compute the distances between the corresponding cameras, and obtain the DTE by taking the average of the mean and root-mean-square (RMS) distance. This metric is an attractive alternative to the ATE, in that it is capable of discerning the varying trajectory accuracy as the inlier trajectory error or the number of outliers varies. Using the similar idea, we also propose a novel rotation error metric, named Discernible Rotation Error (DRE), which has similar advantages to the DTE. Furthermore, we propose a simple yet effective method for calibrating the camera-to-marker rotation, which is needed for the computation of our metrics. Our methods are verified through extensive simulations.

HARA: A Hierarchical Approach for Robust Rotation Averaging

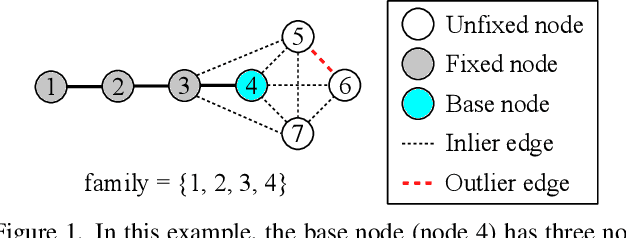
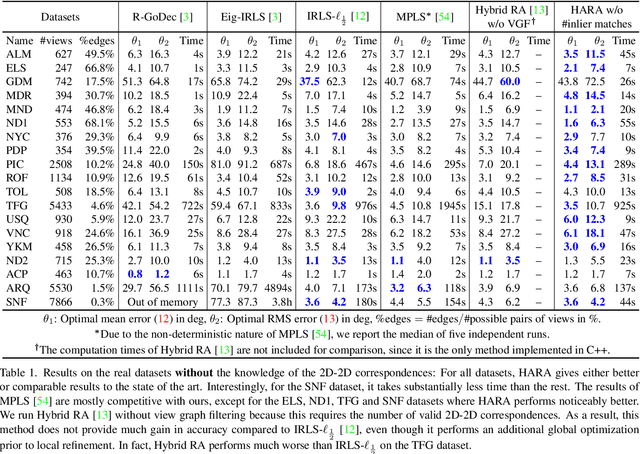
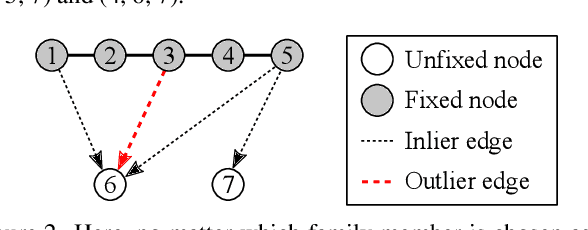
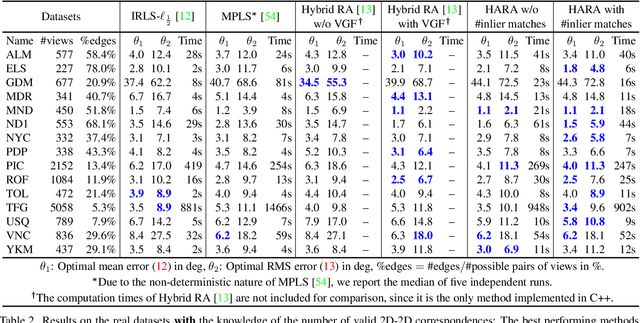
We propose a novel hierarchical approach for multiple rotation averaging, dubbed HARA. Our method incrementally initializes the rotation graph based on a hierarchy of triplet support. The key idea is to build a spanning tree by prioritizing the edges with many strong triplet supports and gradually adding those with weaker and fewer supports. This reduces the risk of adding outliers in the spanning tree. As a result, we obtain a robust initial solution that enables us to filter outliers prior to nonlinear optimization. With minimal modification, our approach can also integrate the knowledge of the number of valid 2D-2D correspondences. We perform extensive evaluations on both synthetic and real datasets, demonstrating state-of-the-art results.

Rotation-Only Bundle Adjustment

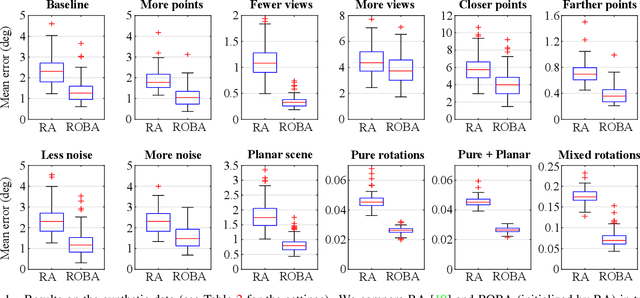
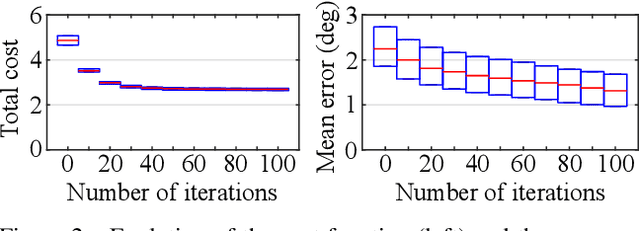
We propose a novel method for estimating the global rotations of the cameras independently of their positions and the scene structure. When two calibrated cameras observe five or more of the same points, their relative rotation can be recovered independently of the translation. We extend this idea to multiple views, thereby decoupling the rotation estimation from the translation and structure estimation. Our approach provides several benefits such as complete immunity to inaccurate translations and structure, and the accuracy improvement when used with rotation averaging. We perform extensive evaluations on both synthetic and real datasets, demonstrating consistent and significant gains in accuracy when used with the state-of-the-art rotation averaging method.

Geometric Interpretations of the Normalized Epipolar Error

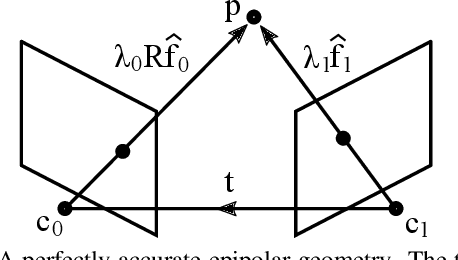
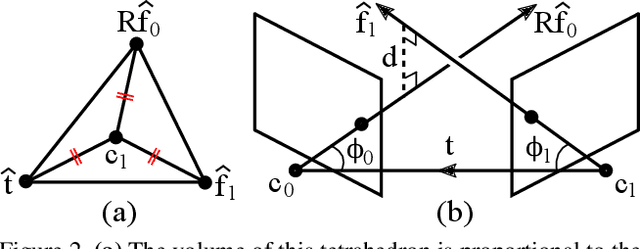
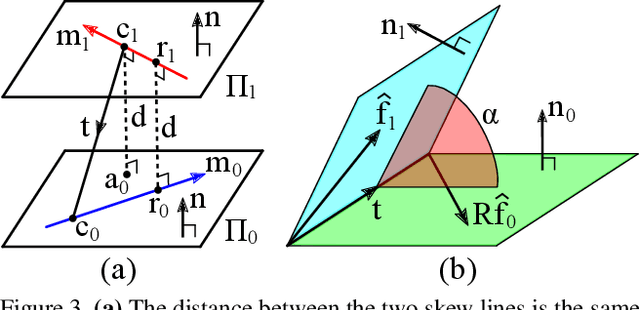
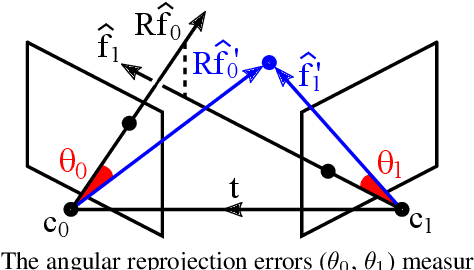
In this work, we provide geometric interpretations of the normalized epipolar error. Most notably, we show that it is directly related to the following quantities: (1) the shortest distance between the two backprojected rays, (2) the dihedral angle between the two bounding epipolar planes, and (3) the $L_1$-optimal angular reprojection error.

Robust Uncertainty-Aware Multiview Triangulation

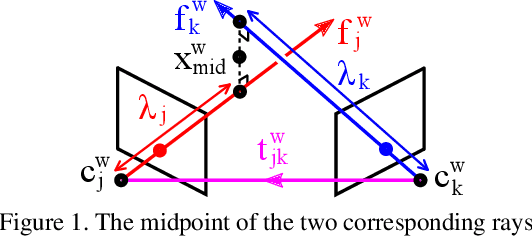
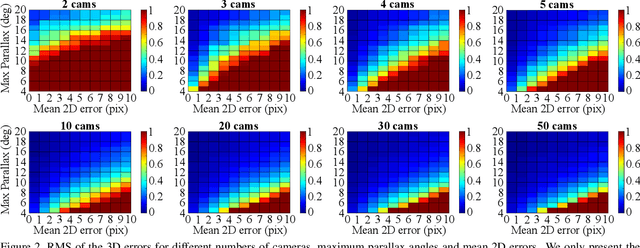
We propose a robust and efficient method for multiview triangulation and uncertainty estimation. Our contribution is threefold: First, we propose an outlier rejection scheme using two-view RANSAC with the midpoint method. By prescreening the two-view samples prior to triangulation, we achieve the state-of-the-art efficiency. Second, we compare different local optimization methods for refining the initial solution and the inlier set. With an iterative update of the inlier set, we show that the optimization provides significant improvement in accuracy and robustness. Third, we model the uncertainty of a triangulated point as a function of three factors: the number of cameras, the mean reprojection error and the maximum parallax angle. Learning this model allows us to quickly interpolate the uncertainty at test time. We validate our method through an extensive evaluation.

Robust Single Rotation Averaging

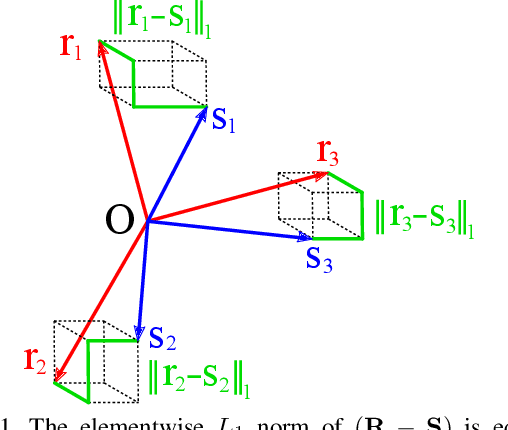
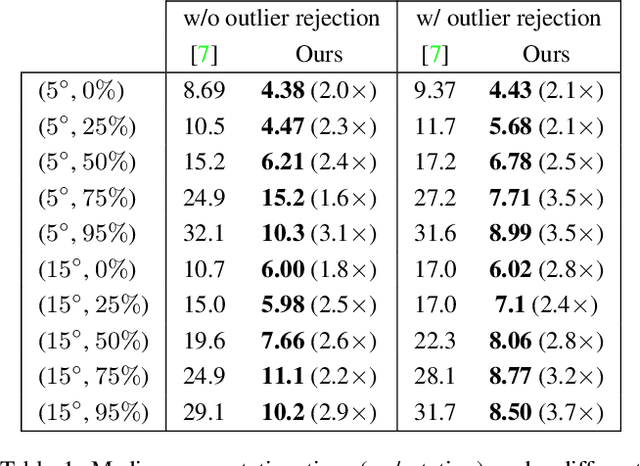
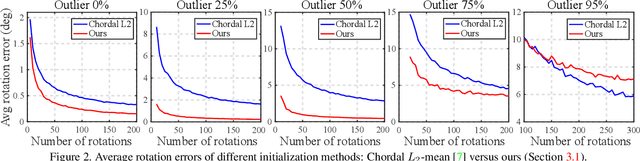
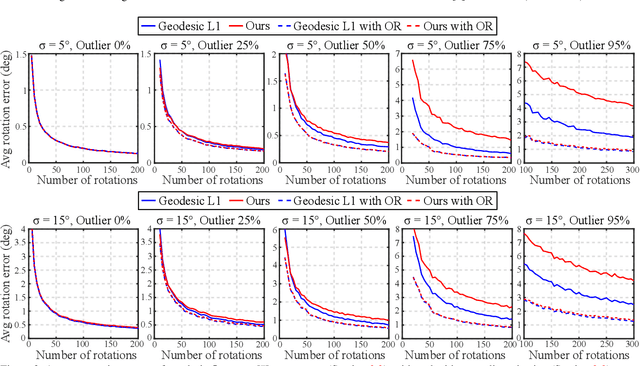
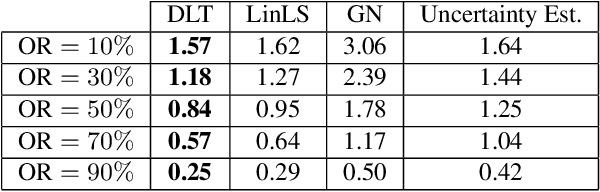
We propose a novel method for single rotation averaging using the Weiszfeld algorithm. Our contribution is threefold: First, we propose a robust initialization based on the elementwise median of the input rotation matrices. Our initial solution is more accurate and robust than the commonly used chordal $L_2$-mean. Second, we propose an outlier rejection scheme that can be incorporated in the Weiszfeld algorithm to improve the robustness of $L_1$ rotation averaging. Third, we propose a method for approximating the chordal $L_1$-mean using the Weiszfeld algorithm. An extensive evaluation shows that both our method and the state of the art perform equally well with the proposed outlier rejection scheme, but ours is $2-4$ times faster.

RGB-D Odometry and SLAM

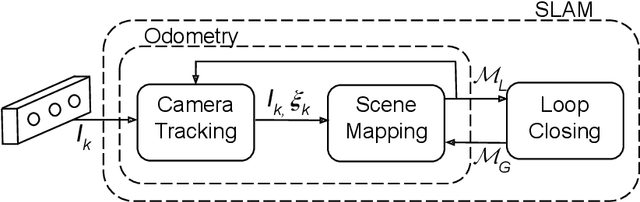
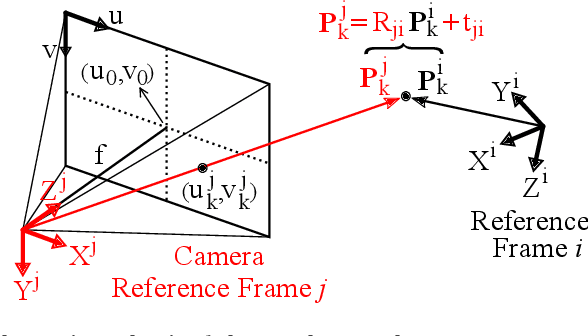
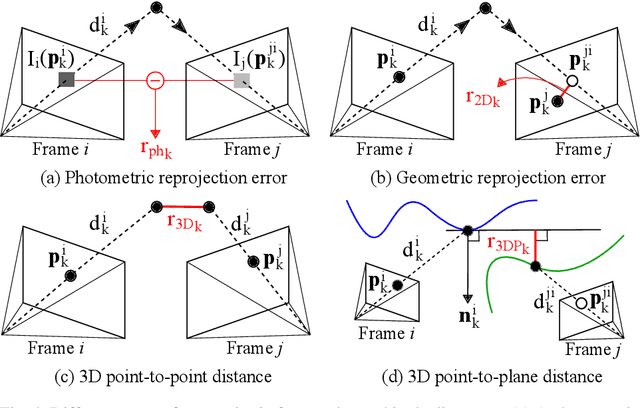
The emergence of modern RGB-D sensors had a significant impact in many application fields, including robotics, augmented reality (AR) and 3D scanning. They are low-cost, low-power and low-size alternatives to traditional range sensors such as LiDAR. Moreover, unlike RGB cameras, RGB-D sensors provide the additional depth information that removes the need of frame-by-frame triangulation for 3D scene reconstruction. These merits have made them very popular in mobile robotics and AR, where it is of great interest to estimate ego-motion and 3D scene structure. Such spatial understanding can enable robots to navigate autonomously without collisions and allow users to insert virtual entities consistent with the image stream. In this chapter, we review common formulations of odometry and Simultaneous Localization and Mapping (known by its acronym SLAM) using RGB-D stream input. The two topics are closely related, as the former aims to track the incremental camera motion with respect to a local map of the scene, and the latter to jointly estimate the camera trajectory and the global map with consistency. In both cases, the standard approaches minimize a cost function using nonlinear optimization techniques. This chapter consists of three main parts: In the first part, we introduce the basic concept of odometry and SLAM and motivate the use of RGB-D sensors. We also give mathematical preliminaries relevant to most odometry and SLAM algorithms. In the second part, we detail the three main components of SLAM systems: camera pose tracking, scene mapping and loop closing. For each component, we describe different approaches proposed in the literature. In the final part, we provide a brief discussion on advanced research topics with the references to the state-of-the-art.