Generalized Adversarial Distances to Efficiently Discover Classifier Errors

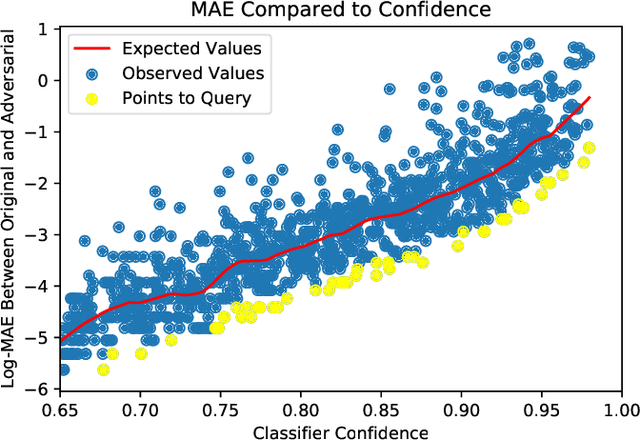
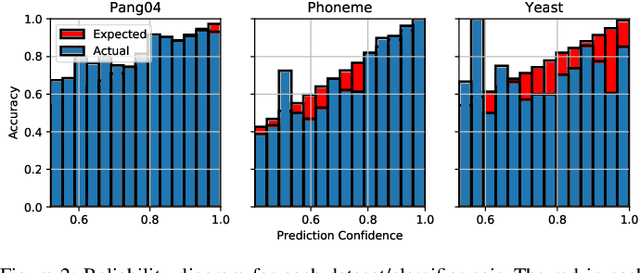
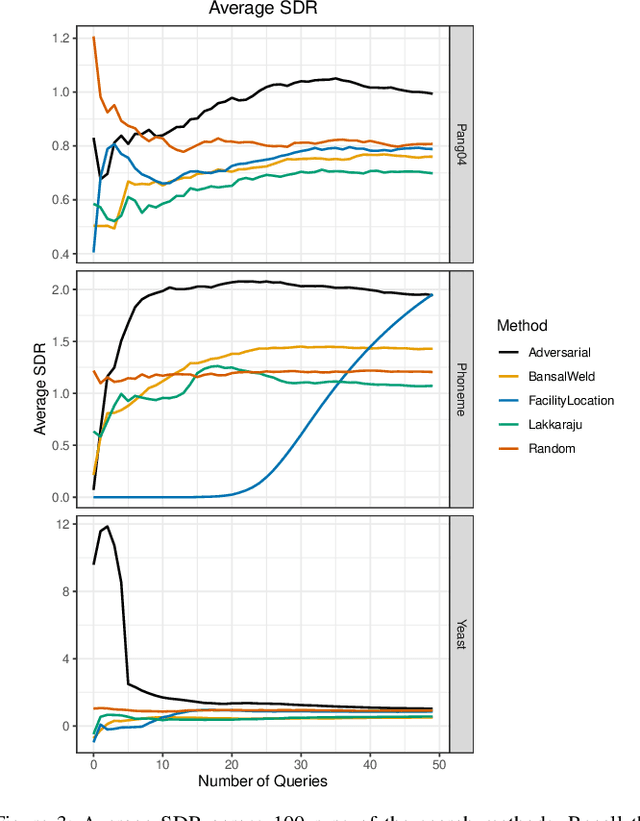
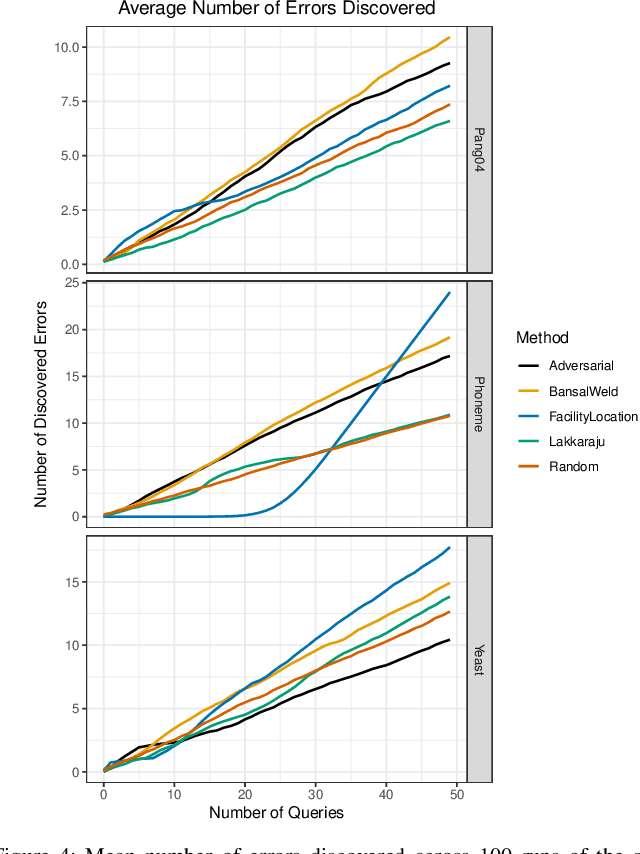
Given a black-box classification model and an unlabeled evaluation dataset from some application domain, efficient strategies need to be developed to evaluate the model. Random sampling allows a user to estimate metrics like accuracy, precision, and recall, but may not provide insight to high-confidence errors. High-confidence errors are rare events for which the model is highly confident in its prediction, but is wrong. Such errors can represent costly mistakes and should be explicitly searched for. In this paper we propose a generalization to the Adversarial Distance search that leverages concepts from adversarial machine learning to identify predictions for which a classifier may be overly confident. These predictions are useful instances to sample when looking for high-confidence errors because they are prone to a higher rate of error than expected. Our generalization allows Adversarial Distance to be applied to any classifier or data domain. Experimental results show that the generalized method finds errors at rates greater than expected given the confidence of the sampled predictions, and outperforms competing methods.

Harnessing Adversarial Distances to Discover High-Confidence Errors

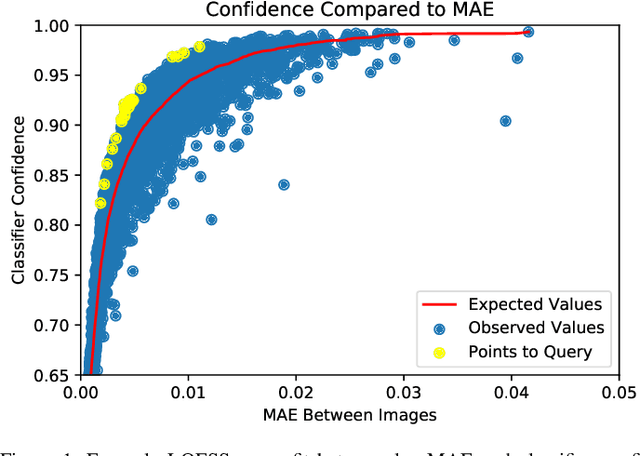
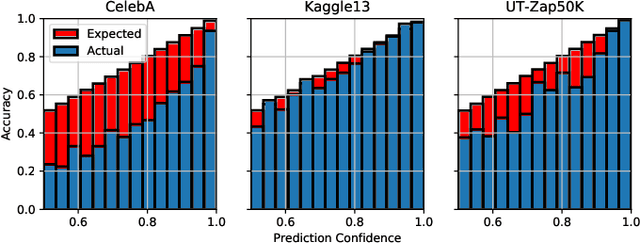
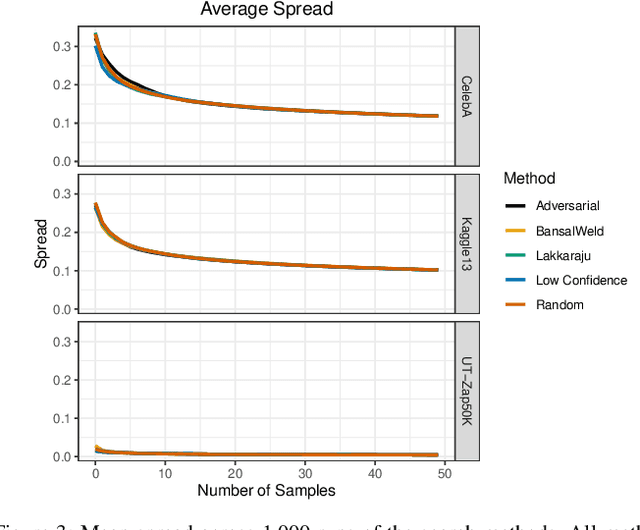
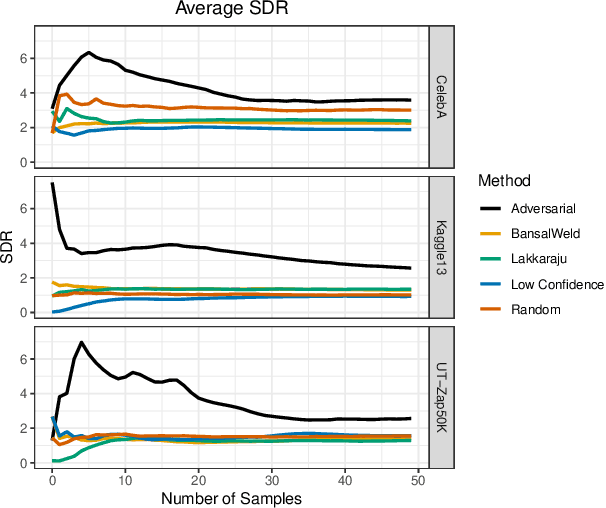
Given a deep neural network image classification model that we treat as a black box, and an unlabeled evaluation dataset, we develop an efficient strategy by which the classifier can be evaluated. Randomly sampling and labeling instances from an unlabeled evaluation dataset allows traditional performance measures like accuracy, precision, and recall to be estimated. However, random sampling may miss rare errors for which the model is highly confident in its prediction, but wrong. These high-confidence errors can represent costly mistakes, and therefore should be explicitly searched for. Past works have developed search techniques to find classification errors above a specified confidence threshold, but ignore the fact that errors should be expected at confidence levels anywhere below 100\%. In this work, we investigate the problem of finding errors at rates greater than expected given model confidence. Additionally, we propose a query-efficient and novel search technique that is guided by adversarial perturbations to find these mistakes in black box models. Through rigorous empirical experimentation, we demonstrate that our Adversarial Distance search discovers high-confidence errors at a rate greater than expected given model confidence.