The Geometric Structure of Externally Actuated Planar Locomoting Systems in Ambient Media

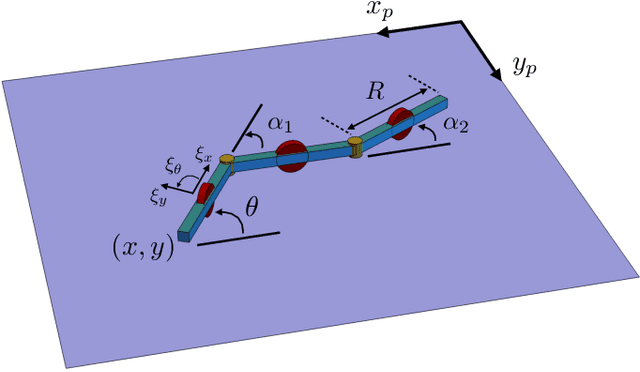
Robots often interact with the world via attached parts such as wheels, joints, or appendages. In many systems, these interactions, and the manner in which they lead to locomotion, can be understood using the machinery of geometric mechanics, explaining how inputs in the shape space of a robot affect motion in its configuration space and the configuration space of its environment. In this paper we consider an opposite type of locomotion, wherein robots are influenced actively by interactions with an externally forced ambient medium. We investigate two examples of externally actuated systems; one for which locomotion is governed by a principal connection, and is usually considered to possess no drift dynamics, and another for which no such connection exists, with drift inherent in its locomotion. For the driftless system, we develop geometric tools based on previously understood internally actuated versions of the system and demonstrate their use for motion planning under external actuation. For the system possessing drift, we employ nonholonomic reduction to obtain a reduced representation of the system dynamics, illustrate geometric features conducive to studying locomotion, and derive strategies for external actuation.