Sayan Gul
Learning to select computations
Aug 07, 2018

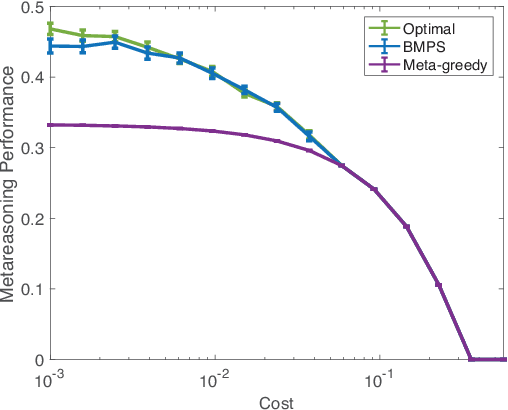

Abstract:The efficient use of limited computational resources is an essential ingredient of intelligence. Selecting computations optimally according to rational metareasoning would achieve this, but this is computationally intractable. Inspired by psychology and neuroscience, we propose the first concrete and domain-general learning algorithm for approximating the optimal selection of computations: Bayesian metalevel policy search (BMPS). We derive this general, sample-efficient search algorithm for a computation-selecting metalevel policy based on the insight that the value of information lies between the myopic value of information and the value of perfect information. We evaluate BMPS on three increasingly difficult metareasoning problems: when to terminate computation, how to allocate computation between competing options, and planning. Across all three domains, BMPS achieved near-optimal performance and compared favorably to previously proposed metareasoning heuristics. Finally, we demonstrate the practical utility of BMPS in an emergency management scenario, even accounting for the overhead of metareasoning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge