Causal Interventions Reveal Shared Structure Across English Filler-Gap Constructions

Large Language Models (LLMs) have emerged as powerful sources of evidence for linguists seeking to develop theories of syntax. In this paper, we argue that causal interpretability methods, applied to LLMs, can greatly enhance the value of such evidence by helping us characterize the abstract mechanisms that LLMs learn to use. Our empirical focus is a set of English filler-gap dependency constructions (e.g., questions, relative clauses). Linguistic theories largely agree that these constructions share many properties. Using experiments based in Distributed Interchange Interventions, we show that LLMs converge on similar abstract analyses of these constructions. These analyses also reveal previously overlooked factors -- relating to frequency, filler type, and surrounding context -- that could motivate changes to standard linguistic theory. Overall, these results suggest that mechanistic, internal analyses of LLMs can push linguistic theory forward.

Models Can and Should Embrace the Communicative Nature of Human-Generated Math

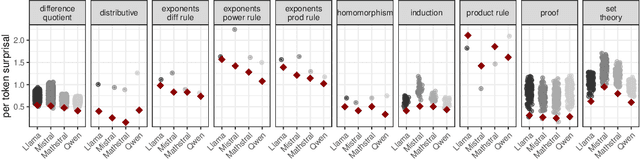
Math is constructed by people for people: just as natural language corpora reflect not just propositions but the communicative goals of language users, the math data that models are trained on reflects not just idealized mathematical entities but rich communicative intentions. While there are important advantages to treating math in a purely symbolic manner, we here hypothesize that there are benefits to treating math as situated linguistic communication and that language models are well suited for this goal, in ways that are not fully appreciated. We illustrate these points with two case studies. First, we ran an experiment in which we found that language models interpret the equals sign in a humanlike way -- generating systematically different word problems for the same underlying equation arranged in different ways. Second, we found that language models prefer proofs to be ordered in naturalistic ways, even though other orders would be logically equivalent. We advocate for AI systems that learn from and represent the communicative intentions latent in human-generated math.