Language Conditioning Improves Accuracy of Aircraft Goal Prediction in Untowered Airspace

Autonomous aircraft must safely operate in untowered airspace, where coordination relies on voice-based communication among human pilots. Safe operation requires an aircraft to predict the intent, and corresponding goal location, of other aircraft. This paper introduces a multimodal framework for aircraft goal prediction that integrates natural language understanding with spatial reasoning to improve autonomous decision-making in such environments. We leverage automatic speech recognition and large language models to transcribe and interpret pilot radio calls, identify aircraft, and extract discrete intent labels. These intent labels are fused with observed trajectories to condition a temporal convolutional network and Gaussian mixture model for probabilistic goal prediction. Our method significantly reduces goal prediction error compared to baselines that rely solely on motion history, demonstrating that language-conditioned prediction increases prediction accuracy. Experiments on a real-world dataset from an untowered airport validate the approach and highlight its potential to enable socially aware, language-conditioned robotic motion planning.

Markov Potential Game with Final-time Reach-Avoid Objectives

We formulate a Markov potential game with final-time reach-avoid objectives by integrating potential game theory with stochastic reach-avoid control. Our focus is on multi-player trajectory planning where players maximize the same multi-player reach-avoid objective: the probability of all participants reaching their designated target states by a specified time, while avoiding collisions with one another. Existing approaches require centralized computation of actions via a global policy, which may have prohibitively expensive communication costs. Instead, we focus on approximations of the global policy via local state feedback policies. First, we adapt the recursive single player reach-avoid value iteration to the multi-player framework with local policies, and show that the same recursion holds on the joint state space. To find each player's optimal local policy, the multi-player reach-avoid value function is projected from the joint state to the local state using the other players' occupancy measures. Then, we propose an iterative best response scheme for the multi-player value iteration to converge to a pure Nash equilibrium. We demonstrate the utility of our approach in finding collision-free policies for multi-player motion planning in simulation.

Set-based value operators for non-stationary Markovian environments

This paper analyzes finite state Markov Decision Processes (MDPs) with uncertain parameters in compact sets and re-examines results from robust MDP via set-based fixed point theory. We generalize the Bellman and policy evaluation operators to operators that contract on the space of value functions and denote them as \emph{value operators}. We generalize these value operators to act on the space of value function sets and denote them as \emph{set-based value operators}. We prove that these set-based value operators are contractions in the space of compact value function sets. Leveraging insights from set theory, we generalize the rectangularity condition for the Bellman operator from classic robust MDP literature to a \emph{containment condition} for a generic value operator, which is weaker and can be applied to a larger set of parameter-uncertain MDPs and contractive operators in dynamic programming and reinforcement learning. We prove that both the rectangularity condition and the containment condition sufficiently ensure that the set-based value operator's fixed point set contains its own supremum and infimum elements. For convex and compact sets of uncertain MDP parameters, we show equivalence between the classic robust value function and the supremum of the fixed point set of the set-based Bellman operator. Under dynamically changing MDP parameters in compact sets, we prove a set convergence result for value iteration, which otherwise may not converge to a single value function.

General sum stochastic games with networked information flows

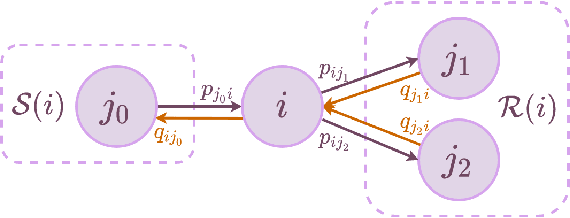
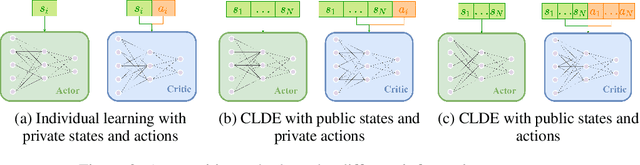
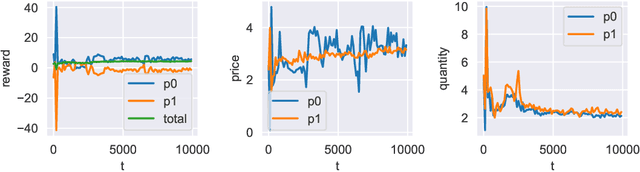
Inspired by applications such as supply chain management, epidemics, and social networks, we formulate a stochastic game model that addresses three key features common across these domains: 1) network-structured player interactions, 2) pair-wise mixed cooperation and competition among players, and 3) limited global information toward individual decision-making. In combination, these features pose significant challenges for black box approaches taken by deep learning-based multi-agent reinforcement learning (MARL) algorithms and deserve more detailed analysis. We formulate a networked stochastic game with pair-wise general sum objectives and asymmetrical information structure, and empirically explore the effects of information availability on the outcomes of different MARL paradigms such as individual learning and centralized learning decentralized execution.