Mapping User Trust in Vision Language Models: Research Landscape, Challenges, and Prospects

The rapid adoption of Vision Language Models (VLMs), pre-trained on large image-text and video-text datasets, calls for protecting and informing users about when to trust these systems. This survey reviews studies on trust dynamics in user-VLM interactions, through a multi-disciplinary taxonomy encompassing different cognitive science capabilities, collaboration modes, and agent behaviours. Literature insights and findings from a workshop with prospective VLM users inform preliminary requirements for future VLM trust studies.

Learning Interpretable Heuristics for WalkSAT

Local search algorithms are well-known methods for solving large, hard instances of the satisfiability problem (SAT). The performance of these algorithms crucially depends on heuristics for setting noise parameters and scoring variables. The optimal setting for these heuristics varies for different instance distributions. In this paper, we present an approach for learning effective variable scoring functions and noise parameters by using reinforcement learning. We consider satisfiability problems from different instance distributions and learn specialized heuristics for each of them. Our experimental results show improvements with respect to both a WalkSAT baseline and another local search learned heuristic.

Extracting Lifted Mutual Exclusion Invariants from Temporal Planning Domains

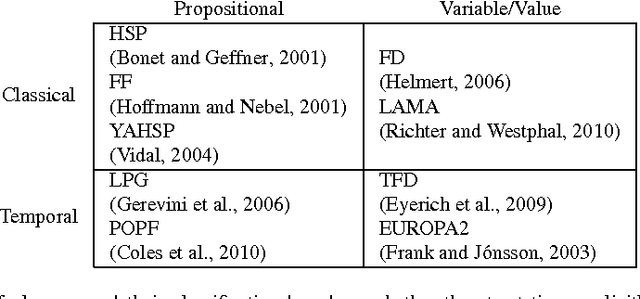
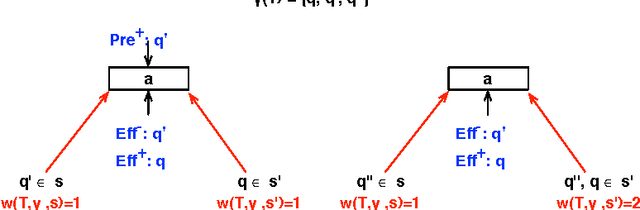
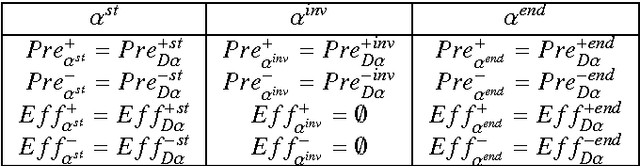
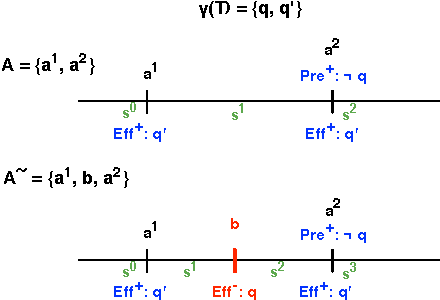
We present a technique for automatically extracting mutual exclusion invariants from temporal planning instances. It first identifies a set of invariant templates by inspecting the lifted representation of the domain and then checks these templates against properties that assure invariance. Our technique builds on other approaches to invariant synthesis presented in the literature, but departs from their limited focus on instantaneous actions by addressing temporal domains. To deal with time, we formulate invariance conditions that account for the entire structure of the actions and the possible concurrent interactions between them. As a result, we construct a significantly more comprehensive technique than previous methods, which is able to find not only invariants for temporal domains, but also a broader set of invariants for non-temporal domains. The experimental results reported in this paper provide evidence that identifying a broader set of invariants results in the generation of fewer multi-valued state variables with larger domains. We show that, in turn, this reduction in the number of variables reflects positively on the performance of a number of temporal planners that use a variable/value representation by significantly reducing their running time.