Robust Neural IDA-PBC: passivity-based stabilization under approximations

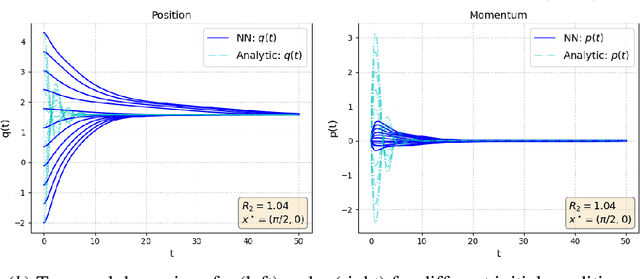
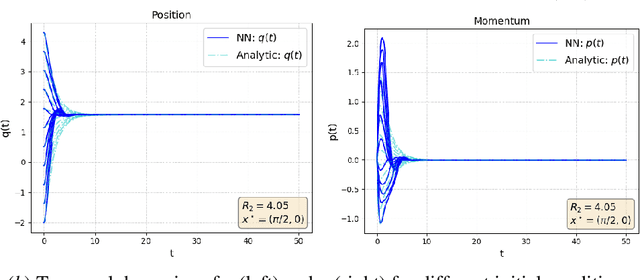
In this paper, we restructure the Neural Interconnection and Damping Assignment - Passivity Based Control (Neural IDA-PBC) design methodology, and we formally analyze its closed-loop properties. Neural IDA-PBC redefines the IDA-PBC design approach as an optimization problem by building on the framework of Physics Informed Neural Networks (PINNs). However, the closed-loop stability and robustness properties under Neural IDA-PBC remain unexplored. To address the issue, we study the behavior of classical IDA-PBC under approximations. Our theoretical analysis allows deriving conditions for practical and asymptotic stability of the desired equilibrium point. Moreover, it extends the Neural IDA-PBC applicability to port-Hamiltonian systems where the matching conditions cannot be solved exactly. Our renewed optimization-based design introduces three significant aspects: i) it involves a novel optimization objective including stability and robustness constraints issued from our theoretical analysis; ii) it employs separate Neural Networks (NNs), which can be structured to reduce the search space to relevant functions; iii) it does not require knowledge about the port-Hamiltonian formulation of the system's model. Our methodology is validated with simulations on three standard benchmarks: a double pendulum, a nonlinear mass-spring-damper and a cartpole. Notably, classical IDA-PBC designs cannot be analytically derived for the latter.

Total Energy Shaping with Neural Interconnection and Damping Assignment -- Passivity Based Control

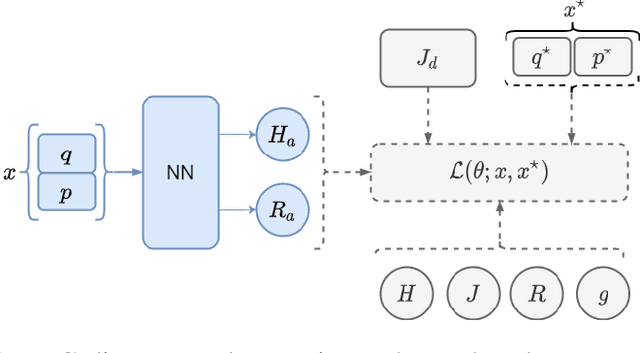
In this work we exploit the universal approximation property of Neural Networks (NNs) to design interconnection and damping assignment (IDA) passivity-based control (PBC) schemes for fully-actuated mechanical systems in the port-Hamiltonian (pH) framework. To that end, we transform the IDA-PBC method into a supervised learning problem that solves the partial differential matching equations, and fulfills equilibrium assignment and Lyapunov stability conditions. A main consequence of this, is that the output of the learning algorithm has a clear control-theoretic interpretation in terms of passivity and Lyapunov stability. The proposed control design methodology is validated for mechanical systems of one and two degrees-of-freedom via numerical simulations.