Rodolfo Reyes-Baez
Total Energy Shaping with Neural Interconnection and Damping Assignment -- Passivity Based Control
Dec 24, 2021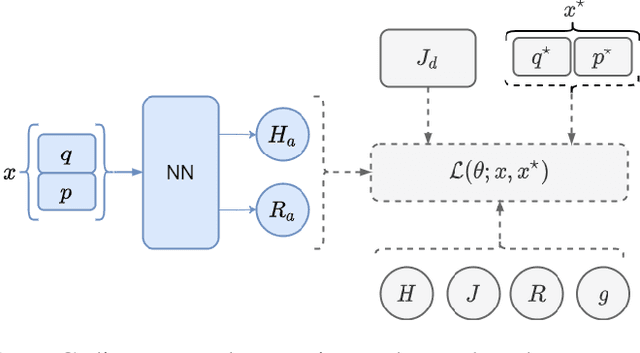
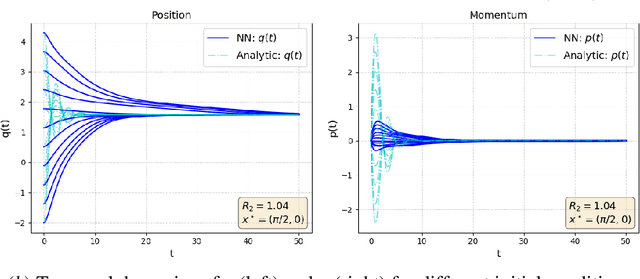
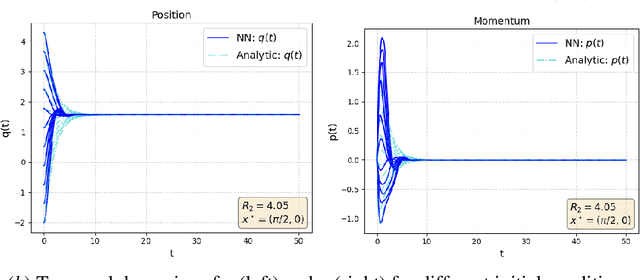

Abstract:In this work we exploit the universal approximation property of Neural Networks (NNs) to design interconnection and damping assignment (IDA) passivity-based control (PBC) schemes for fully-actuated mechanical systems in the port-Hamiltonian (pH) framework. To that end, we transform the IDA-PBC method into a supervised learning problem that solves the partial differential matching equations, and fulfills equilibrium assignment and Lyapunov stability conditions. A main consequence of this, is that the output of the learning algorithm has a clear control-theoretic interpretation in terms of passivity and Lyapunov stability. The proposed control design methodology is validated for mechanical systems of one and two degrees-of-freedom via numerical simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge