Santiago Aja-Fernandez
aDWI-BIDS: an extension to the brain imaging data structure for advanced diffusion weighted imaging
Apr 12, 2021

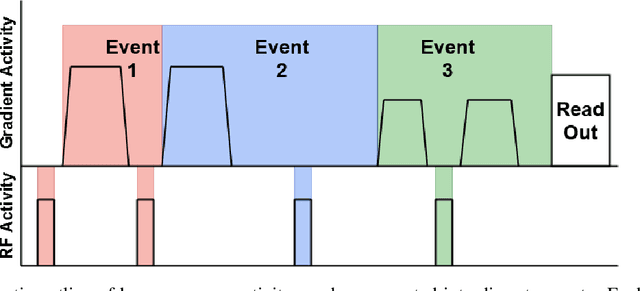
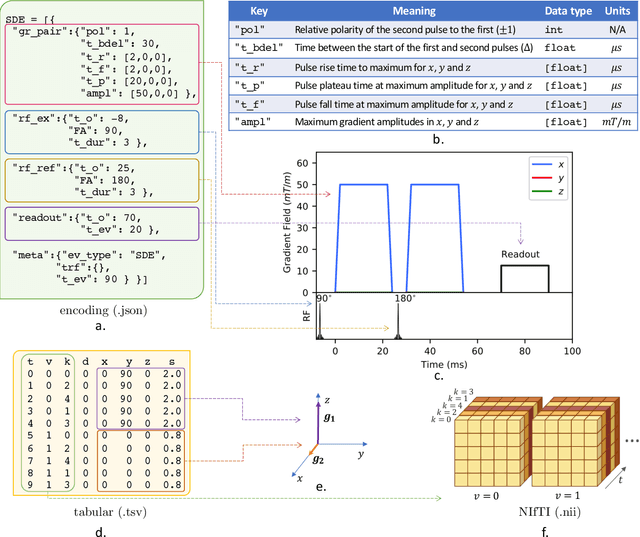
Abstract:Diffusion weighted imaging techniques permit us to infer microstructural detail in biological tissue in vivo and noninvasively. Modern sequences are based on advanced diffusion encoding schemes, allowing probing of more revealing measures of tissue microstructure than the standard apparent diffusion coefficient or fractional anisotropy. Though these methods may result in faster or more revealing acquisitions, they generally demand prior knowledge of sequence-specific parameters for which there is no accepted sharing standard. Here, we present a metadata labelling scheme suitable for the needs of developers and users within the diffusion neuroimaging community alike: a lightweight, unambiguous parametric map relaying acqusition parameters. This extensible scheme supports a wide spectrum of diffusion encoding methods, from single diffusion encoding to highly complex sequences involving arbitrary gradient waveforms. Built under the brain imaging data structure (BIDS), it allows storage of advanced diffusion MRI data comprehensively alongside any other neuroimaging information, facilitating processing pipelines and multimodal analyses. We illustrate the usefulness of this BIDS-extension with a range of example data, and discuss the extension's impact on pre- and post-processing software.
Statistical Noise Analysis in SENSE Parallel MRI
Feb 17, 2014



Abstract:A complete first and second order statistical characterization of noise in SENSE reconstructed data is proposed. SENSE acquisitions have usually been modeled as Rician distributed, since the data reconstruction takes place into the spatial domain, where Gaussian noise is assumed. However, this model just holds for the first order statistics and obviates other effects induced by coils correlations and the reconstruction interpolation. Those effects are properly taken into account in this study, in order to fully justify a final SENSE noise model. As a result, some interesting features of the reconstructed image arise: (1) There is a strong correlation between adjacent lines. (2) The resulting distribution is non-stationary and therefore the variance of noise will vary from point to point across the image. Closed equations for the calculation of the variance of noise and the correlation coefficient between lines are proposed. The proposed model is totally compatible with g-factor formulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge