Curse of Dimensionality in Neural Network Optimization

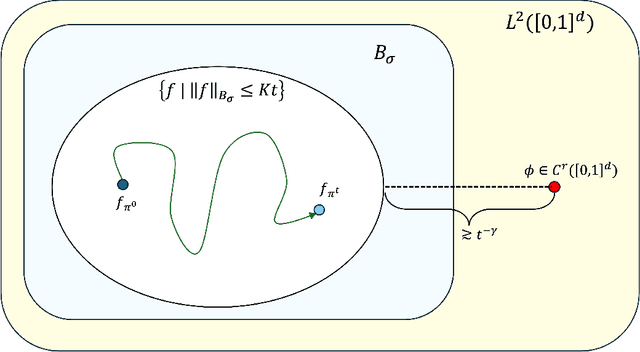
The curse of dimensionality in neural network optimization under the mean-field regime is studied. It is demonstrated that when a shallow neural network with a Lipschitz continuous activation function is trained using either empirical or population risk to approximate a target function that is $r$ times continuously differentiable on $[0,1]^d$, the population risk may not decay at a rate faster than $t^{-\frac{4r}{d-2r}}$, where $t$ is an analog of the total number of optimization iterations. This result highlights the presence of the curse of dimensionality in the optimization computation required to achieve a desired accuracy. Instead of analyzing parameter evolution directly, the training dynamics are examined through the evolution of the parameter distribution under the 2-Wasserstein gradient flow. Furthermore, it is established that the curse of dimensionality persists when a locally Lipschitz continuous activation function is employed, where the Lipschitz constant in $[-x,x]$ is bounded by $O(x^\delta)$ for any $x \in \mathbb{R}$. In this scenario, the population risk is shown to decay at a rate no faster than $t^{-\frac{(4+2\delta)r}{d-2r}}$. To the best of our knowledge, this work is the first to analyze the impact of function smoothness on the curse of dimensionality in neural network optimization theory.

Frame Quantization of Neural Networks

We present a post-training quantization algorithm with error estimates relying on ideas originating from frame theory. Specifically, we use first-order Sigma-Delta ($\Sigma\Delta$) quantization for finite unit-norm tight frames to quantize weight matrices and biases in a neural network. In our scenario, we derive an error bound between the original neural network and the quantized neural network in terms of step size and the number of frame elements. We also demonstrate how to leverage the redundancy of frames to achieve a quantized neural network with higher accuracy.