Curse of Dimensionality in Neural Network Optimization
Paper and Code
Feb 07, 2025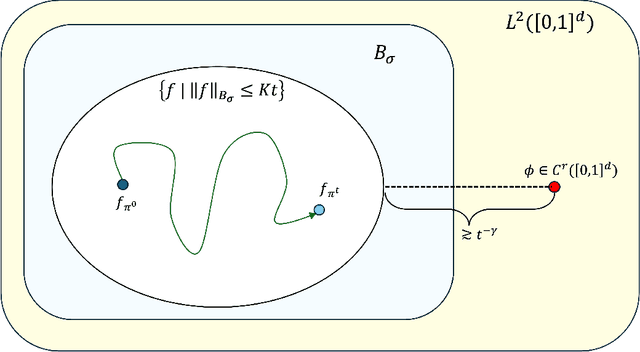
The curse of dimensionality in neural network optimization under the mean-field regime is studied. It is demonstrated that when a shallow neural network with a Lipschitz continuous activation function is trained using either empirical or population risk to approximate a target function that is $r$ times continuously differentiable on $[0,1]^d$, the population risk may not decay at a rate faster than $t^{-\frac{4r}{d-2r}}$, where $t$ is an analog of the total number of optimization iterations. This result highlights the presence of the curse of dimensionality in the optimization computation required to achieve a desired accuracy. Instead of analyzing parameter evolution directly, the training dynamics are examined through the evolution of the parameter distribution under the 2-Wasserstein gradient flow. Furthermore, it is established that the curse of dimensionality persists when a locally Lipschitz continuous activation function is employed, where the Lipschitz constant in $[-x,x]$ is bounded by $O(x^\delta)$ for any $x \in \mathbb{R}$. In this scenario, the population risk is shown to decay at a rate no faster than $t^{-\frac{(4+2\delta)r}{d-2r}}$. To the best of our knowledge, this work is the first to analyze the impact of function smoothness on the curse of dimensionality in neural network optimization theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge