Belief Base Revision for Further Improvement of Unified Answer Set Programming

A belief base revision is developed. The belief base is represented using Unified Answer Set Programs which is capable of representing imprecise and uncertain information and perform nonomonotonic reasoning with them. The base revision operator is developed using Removed Set Revision strategy. The operator is characterized with respect to the postulates for base revisions operator satisfies.

Modeling Uncertainty and Imprecision in Nonmonotonic Reasoning using Fuzzy Numbers

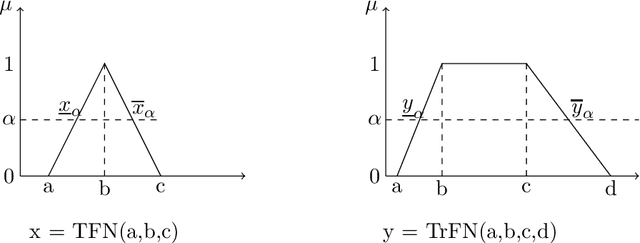
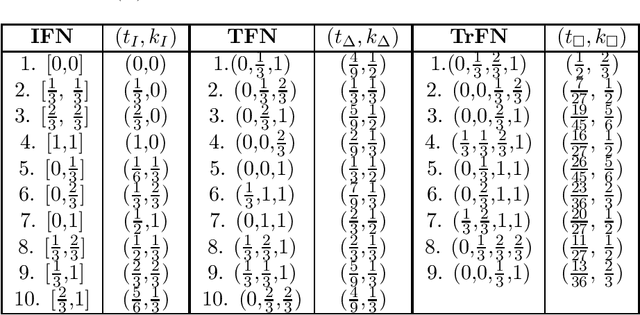
To deal with uncertainty in reasoning, interval-valued logic has been developed. But uniform intervals cannot capture the difference in degrees of belief for different values in the interval. To salvage the problem triangular and trapezoidal fuzzy numbers are used as the set of truth values along with traditional intervals. Preorder-based truth and knowledge ordering are defined over the set of fuzzy numbers defined over $[0,1]$. Based on this enhanced set of epistemic states, an answer set framework is developed, with properly defined logical connectives. This type of framework is efficient in knowledge representation and reasoning with vague and uncertain information under nonmonotonic environment where rules may posses exceptions.

A Unified Framework for Nonmonotonic Reasoning with Vagueness and Uncertainty

An answer set programming paradigm is proposed that supports nonmonotonic reasoning with vague and uncertain information. The system can represent and reason with prioritized rules, rules with exceptions. An iterative method for answer set computation is proposed. The terminating conditions are identified for a class of logic programs using the notion of difference equations. In order to obtain the difference equations the set of rules are depicted by a signal-flow-graph like structure.

Preorder-Based Triangle: A Modified Version of Bilattice-Based Triangle for Belief Revision in Nonmonotonic Reasoning

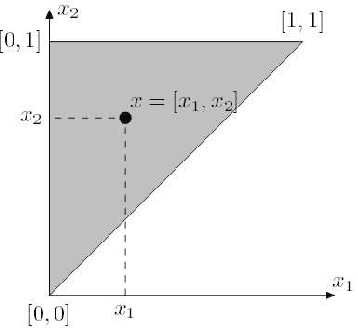
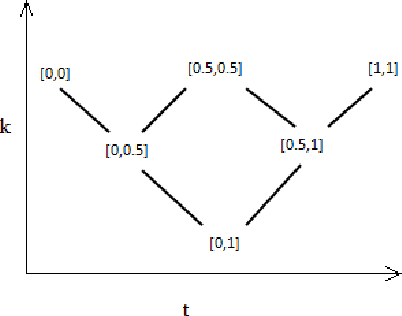
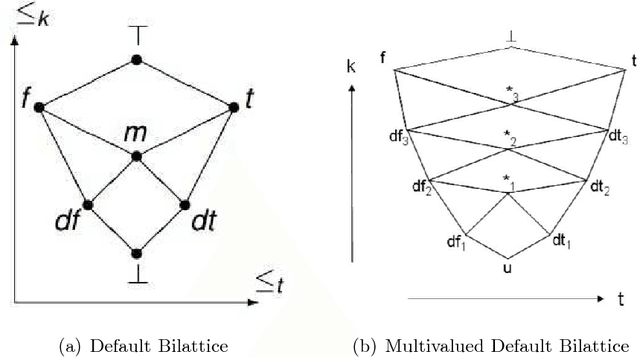
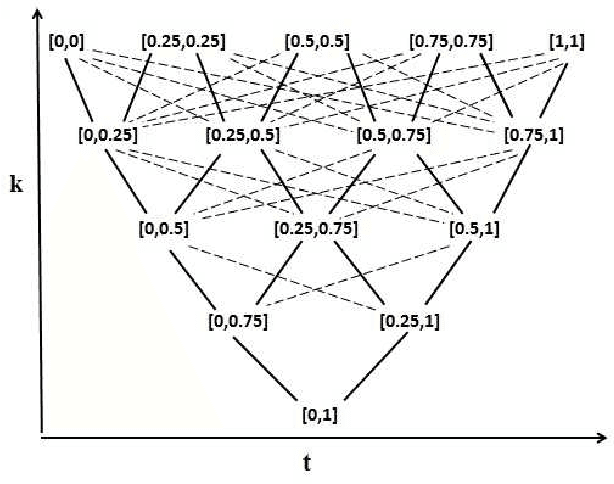
Bilattice-based triangle provides an elegant algebraic structure for reasoning with vague and uncertain information. But the truth and knowledge ordering of intervals in bilattice-based triangle can not handle repetitive belief revisions which is an essential characteristic of nonmonotonic reasoning. Moreover the ordering induced over the intervals by the bilattice-based triangle is not sometimes intuitive. In this work, we construct an alternative algebraic structure, namely preorder-based triangle and we formulate proper logical connectives for this. It is also demonstrated that Preorder-based triangle serves to be a better alternative to the bilattice-based triangle for reasoning in application areas, that involve nonmonotonic fuzzy reasoning with uncertain information.