Strengthening Consistency Results in Modal Logic

A fundamental question asked in modal logic is whether a given theory is consistent. But consistent with what? A typical way to address this question identifies a choice of background knowledge axioms (say, S4, D, etc.) and then shows the assumptions codified by the theory in question to be consistent with those background axioms. But determining the specific choice and division of background axioms is, at least sometimes, little more than tradition. This paper introduces **generic theories** for propositional modal logic to address consistency results in a more robust way. As building blocks for background knowledge, generic theories provide a standard for categorical determinations of consistency. We argue that the results and methods of this paper help to elucidate problems in epistemology and enjoy sufficient scope and power to have purchase on problems bearing on modalities in judgement, inference, and decision making.

Universal Agent Mixtures and the Geometry of Intelligence

Inspired by recent progress in multi-agent Reinforcement Learning (RL), in this work we examine the collective intelligent behaviour of theoretical universal agents by introducing a weighted mixture operation. Given a weighted set of agents, their weighted mixture is a new agent whose expected total reward in any environment is the corresponding weighted average of the original agents' expected total rewards in that environment. Thus, if RL agent intelligence is quantified in terms of performance across environments, the weighted mixture's intelligence is the weighted average of the original agents' intelligences. This operation enables various interesting new theorems that shed light on the geometry of RL agent intelligence, namely: results about symmetries, convex agent-sets, and local extrema. We also show that any RL agent intelligence measure based on average performance across environments, subject to certain weak technical conditions, is identical (up to a constant factor) to performance within a single environment dependent on said intelligence measure.

Extending Environments To Measure Self-Reflection In Reinforcement Learning

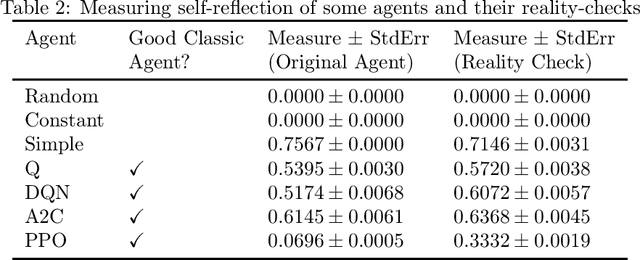
We consider an extended notion of reinforcement learning in which the environment can simulate the agent and base its outputs on the agent's hypothetical behavior. Since good performance usually requires paying attention to whatever things the environment's outputs are based on, we argue that for an agent to achieve on-average good performance across many such extended environments, it is necessary for the agent to self-reflect. Thus, an agent's self-reflection ability can be numerically estimated by running the agent through a battery of extended environments. We are simultaneously releasing an open-source library of extended environments to serve as proof-of-concept of this technique. As the library is first-of-kind, we have avoided the difficult problem of optimizing it. Instead we have chosen environments with interesting properties. Some seem paradoxical, some lead to interesting thought experiments, some are even suggestive of how self-reflection might have evolved in nature. We give examples and introduce a simple transformation which experimentally seems to increase self-reflection.

Reward-Punishment Symmetric Universal Intelligence

Can an agent's intelligence level be negative? We extend the Legg-Hutter agent-environment framework to include punishments and argue for an affirmative answer to that question. We show that if the background encodings and Universal Turing Machine (UTM) admit certain Kolmogorov complexity symmetries, then the resulting Legg-Hutter intelligence measure is symmetric about the origin. In particular, this implies reward-ignoring agents have Legg-Hutter intelligence 0 according to such UTMs.

The Archimedean trap: Why traditional reinforcement learning will probably not yield AGI

After generalizing the Archimedean property of real numbers in such a way as to make it adaptable to non-numeric structures, we demonstrate that the real numbers cannot be used to accurately measure non-Archimedean structures. We argue that, since an agent with Artificial General Intelligence (AGI) should have no problem engaging in tasks that inherently involve non-Archimedean rewards, and since traditional reinforcement learning rewards are real numbers, therefore traditional reinforcement learning cannot lead to AGI. We indicate two possible ways traditional reinforcement learning could be altered to remove this roadblock.

Measuring the intelligence of an idealized mechanical knowing agent

We define a notion of the intelligence level of an idealized mechanical knowing agent. This is motivated by efforts within artificial intelligence research to define real-number intelligence levels of complicated intelligent systems. Our agents are more idealized, which allows us to define a much simpler measure of intelligence level for them. In short, we define the intelligence level of a mechanical knowing agent to be the supremum of the computable ordinals that have codes the agent knows to be codes of computable ordinals. We prove that if one agent knows certain things about another agent, then the former necessarily has a higher intelligence level than the latter. This allows our intelligence notion to serve as a stepping stone to obtain results which, by themselves, are not stated in terms of our intelligence notion (results of potential interest even to readers totally skeptical that our notion correctly captures intelligence). As an application, we argue that these results comprise evidence against the possibility of intelligence explosion (that is, the notion that sufficiently intelligent machines will eventually be capable of designing even more intelligent machines, which can then design even more intelligent machines, and so on).

Intelligence via ultrafilters: structural properties of some intelligence comparators of deterministic Legg-Hutter agents

Legg and Hutter, as well as subsequent authors, considered intelligent agents through the lens of interaction with reward-giving environments, attempting to assign numeric intelligence measures to such agents, with the guiding principle that a more intelligent agent should gain higher rewards from environments in some aggregate sense. In this paper, we consider a related question: rather than measure numeric intelligence of one Legg- Hutter agent, how can we compare the relative intelligence of two Legg-Hutter agents? We propose an elegant answer based on the following insight: we can view Legg-Hutter agents as candidates in an election, whose voters are environments, letting each environment vote (via its rewards) which agent (if either) is more intelligent. This leads to an abstract family of comparators simple enough that we can prove some structural theorems about them. It is an open question whether these structural theorems apply to more practical intelligence measures.