Rolling Horizon based Temporal Decomposition for the Offline Pickup and Delivery Problem with Time Windows

The offline pickup and delivery problem with time windows (PDPTW) is a classical combinatorial optimization problem in the transportation community, which has proven to be very challenging computationally. Due to the complexity of the problem, practical problem instances can be solved only via heuristics, which trade-off solution quality for computational tractability. Among the various heuristics, a common strategy is problem decomposition, that is, the reduction of a large-scale problem into a collection of smaller sub-problems, with spatial and temporal decompositions being two natural approaches. While spatial decomposition has been successful in certain settings, effective temporal decomposition has been challenging due to the difficulty of stitching together the sub-problem solutions across the decomposition boundaries. In this work, we introduce a novel temporal decomposition scheme for solving a class of PDPTWs that have narrow time windows, for which it is able to provide both fast and high-quality solutions. We utilize techniques that have been popularized recently in the context of online dial-a-ride problems along with the general idea of rolling horizon optimization. To the best of our knowledge, this is the first attempt to solve offline PDPTWs using such an approach. To show the performance and scalability of our framework, we use the optimization of paratransit services as a motivating example. We compare our results with an offline heuristic algorithm using Google OR-Tools. In smaller problem instances, the baseline approach is as competitive as our framework. However, in larger problem instances, our framework is more scalable and can provide good solutions to problem instances of varying degrees of difficulty, while the baseline algorithm often fails to find a feasible solution within comparable compute times.

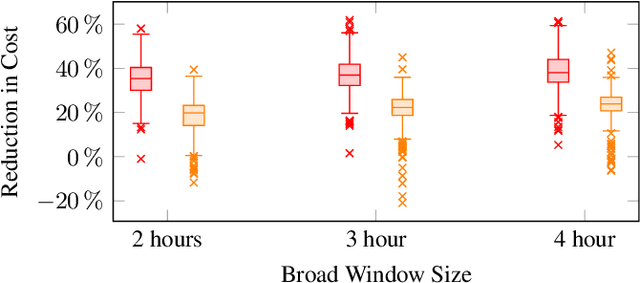
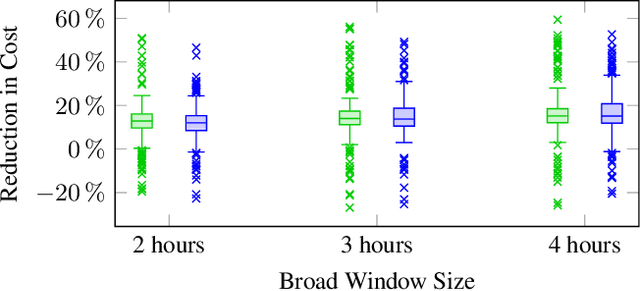
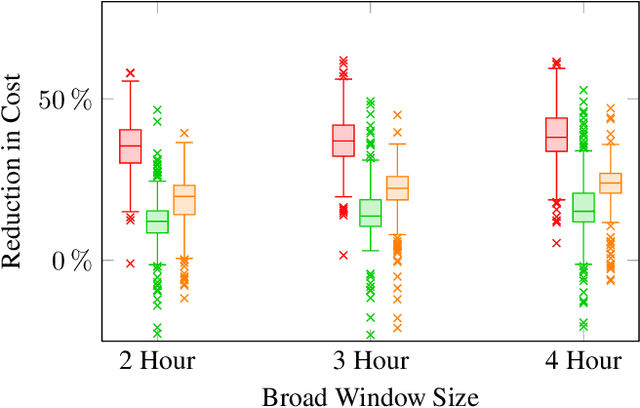
Offline Vehicle Routing Problem with Online Bookings: A Novel Problem Formulation with Applications to Paratransit

Vehicle routing problems (VRPs) can be divided into two major categories: offline VRPs, which consider a given set of trip requests to be served, and online VRPs, which consider requests as they arrive in real-time. Based on discussions with public transit agencies, we identify a real-world problem that is not addressed by existing formulations: booking trips with flexible pickup windows (e.g., 3 hours) in advance (e.g., the day before) and confirming tight pickup windows (e.g., 30 minutes) at the time of booking. Such a service model is often required in paratransit service settings, where passengers typically book trips for the next day over the phone. To address this gap between offline and online problems, we introduce a novel formulation, the offline vehicle routing problem with online bookings. This problem is very challenging computationally since it faces the complexity of considering large sets of requests -- similar to offline VRPs -- but must abide by strict constraints on running time -- similar to online VRPs. To solve this problem, we propose a novel computational approach, which combines an anytime algorithm with a learning-based policy for real-time decisions. Based on a paratransit dataset obtained from the public transit agency of Chattanooga, TN, we demonstrate that our novel formulation and computational approach lead to significantly better outcomes in this setting than existing algorithms.

An Online Approach to Solve the Dynamic Vehicle Routing Problem with Stochastic Trip Requests for Paratransit Services

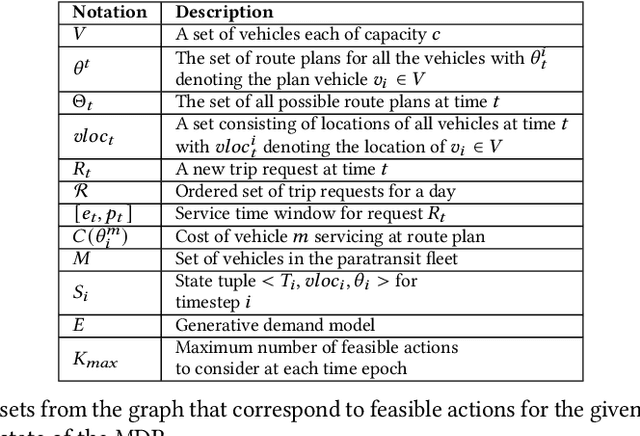
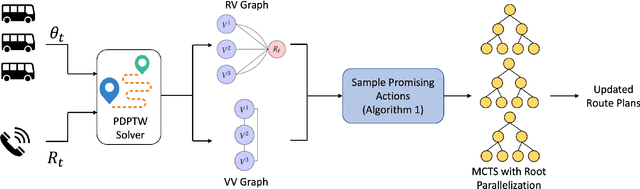
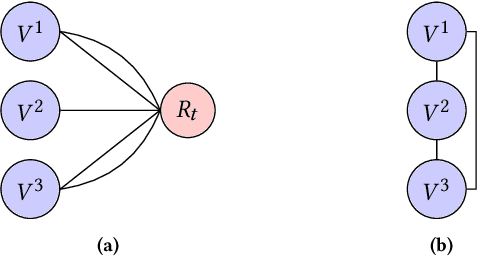
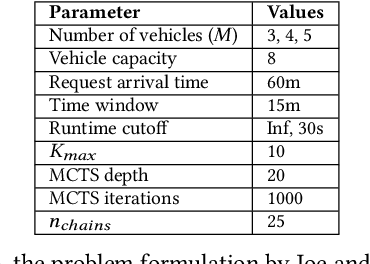
Many transit agencies operating paratransit and microtransit services have to respond to trip requests that arrive in real-time, which entails solving hard combinatorial and sequential decision-making problems under uncertainty. To avoid decisions that lead to significant inefficiency in the long term, vehicles should be allocated to requests by optimizing a non-myopic utility function or by batching requests together and optimizing a myopic utility function. While the former approach is typically offline, the latter can be performed online. We point out two major issues with such approaches when applied to paratransit services in practice. First, it is difficult to batch paratransit requests together as they are temporally sparse. Second, the environment in which transit agencies operate changes dynamically (e.g., traffic conditions), causing estimates that are learned offline to become stale. To address these challenges, we propose a fully online approach to solve the dynamic vehicle routing problem (DVRP) with time windows and stochastic trip requests that is robust to changing environmental dynamics by construction. We focus on scenarios where requests are relatively sparse - our problem is motivated by applications to paratransit services. We formulate DVRP as a Markov decision process and use Monte Carlo tree search to evaluate actions for any given state. Accounting for stochastic requests while optimizing a non-myopic utility function is computationally challenging; indeed, the action space for such a problem is intractably large in practice. To tackle the large action space, we leverage the structure of the problem to design heuristics that can sample promising actions for the tree search. Our experiments using real-world data from our partner agency show that the proposed approach outperforms existing state-of-the-art approaches both in terms of performance and robustness.