Leveraging Semi-Supervised Learning for Fairness using Neural Networks

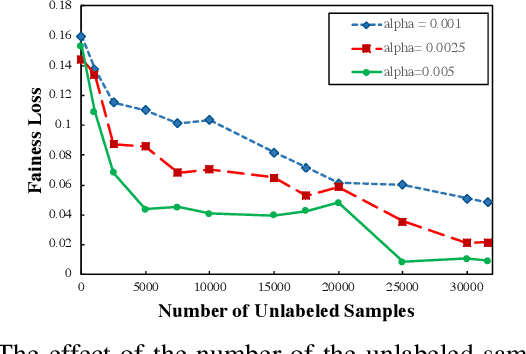
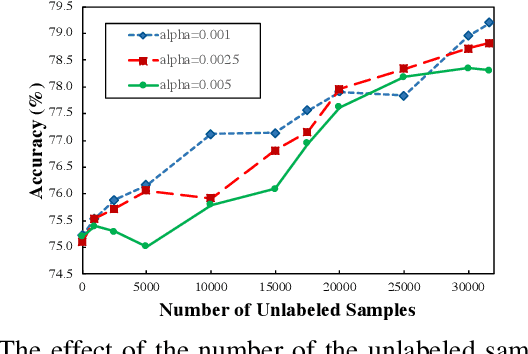
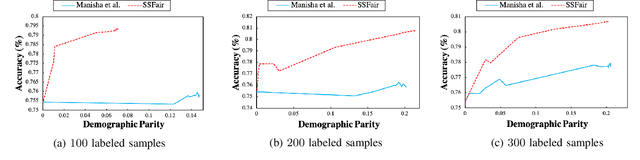
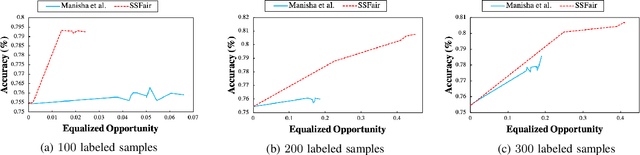
There has been a growing concern about the fairness of decision-making systems based on machine learning. The shortage of labeled data has been always a challenging problem facing machine learning based systems. In such scenarios, semi-supervised learning has shown to be an effective way of exploiting unlabeled data to improve upon the performance of model. Notably, unlabeled data do not contain label information which itself can be a significant source of bias in training machine learning systems. This inspired us to tackle the challenge of fairness by formulating the problem in a semi-supervised framework. In this paper, we propose a semi-supervised algorithm using neural networks benefiting from unlabeled data to not just improve the performance but also improve the fairness of the decision-making process. The proposed model, called SSFair, exploits the information in the unlabeled data to mitigate the bias in the training data.

Practical Newton-Type Distributed Learning using Gradient Based Approximations

We study distributed algorithms for expected loss minimization where the datasets are large and have to be stored on different machines. Often we deal with minimizing the average of a set of convex functions where each function is the empirical risk of the corresponding part of the data. In the distributed setting where the individual data instances can be accessed only on the local machines, there would be a series of rounds of local computations followed by some communication among the machines. Since the cost of the communication is usually higher than the local machine computations, it is important to reduce it as much as possible. However, we should not allow this to make the computation too expensive to become a burden in practice. Using second-order methods could make the algorithms converge faster and decrease the amount of communication needed. There are some successful attempts in developing distributed second-order methods. Although these methods have shown fast convergence, their local computation is expensive and could enjoy more improvement for practical uses. In this study we modify an existing approach, DANE (Distributed Approximate NEwton), in order to improve the computational cost while maintaining the accuracy. We tackle this problem by using iterative methods for solving the local subproblems approximately instead of providing exact solutions for each round of communication. We study how using different iterative methods affect the behavior of the algorithm and try to provide an appropriate tradeoff between the amount of local computation and the required amount of communication. We demonstrate the practicality of our algorithm and compare it to the existing distributed gradient based methods such as SGD.