Fairness in Monotone $k$-submodular Maximization: Algorithms and Applications

Submodular optimization has become increasingly prominent in machine learning and fairness has drawn much attention. In this paper, we propose to study the fair $k$-submodular maximization problem and develop a $\frac{1}{3}$-approximation greedy algorithm with a running time of $\mathcal{O}(knB)$. To the best of our knowledge, our work is the first to incorporate fairness in the context of $k$-submodular maximization, and our theoretical guarantee matches the best-known $k$-submodular maximization results without fairness constraints. In addition, we have developed a faster threshold-based algorithm that achieves a $(\frac{1}{3} - \epsilon)$ approximation with $\mathcal{O}(\frac{kn}{\epsilon} \log \frac{B}{\epsilon})$ evaluations of the function $f$. Furthermore, for both algorithms, we provide approximation guarantees when the $k$-submodular function is not accessible but only can be approximately accessed. We have extensively validated our theoretical findings through empirical research and examined the practical implications of fairness. Specifically, we have addressed the question: ``What is the price of fairness?" through case studies on influence maximization with $k$ topics and sensor placement with $k$ types. The experimental results show that the fairness constraints do not significantly undermine the quality of solutions.

Representing and Reasoning with Multi-Stakeholder Qualitative Preference Queries

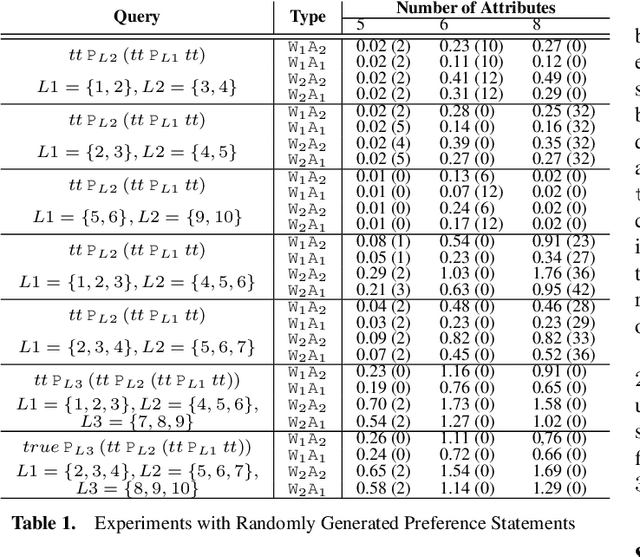
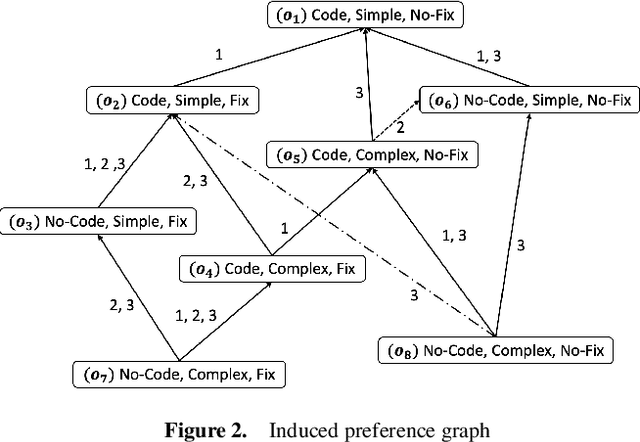
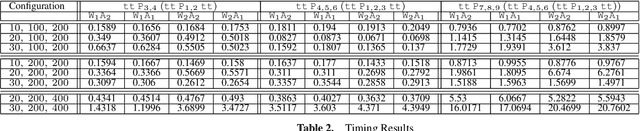
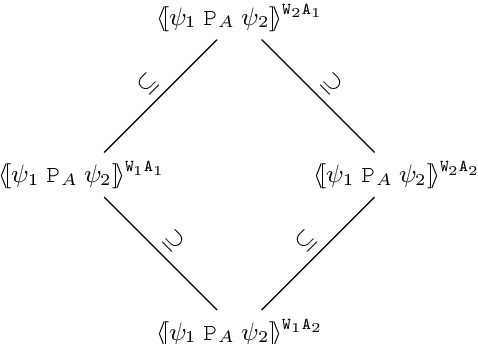
Many decision-making scenarios, e.g., public policy, healthcare, business, and disaster response, require accommodating the preferences of multiple stakeholders. We offer the first formal treatment of reasoning with multi-stakeholder qualitative preferences in a setting where stakeholders express their preferences in a qualitative preference language, e.g., CP-net, CI-net, TCP-net, CP-Theory. We introduce a query language for expressing queries against such preferences over sets of outcomes that satisfy specified criteria, e.g., $\mlangpref{\psi_1}{\psi_2}{A}$ (read loosely as the set of outcomes satisfying $\psi_1$ that are preferred over outcomes satisfying $\psi_2$ by a set of stakeholders $A$). Motivated by practical application scenarios, we introduce and analyze several alternative semantics for such queries, and examine their interrelationships. We provide a provably correct algorithm for answering multi-stakeholder qualitative preference queries using model checking in alternation-free $\mu$-calculus. We present experimental results that demonstrate the feasibility of our approach.

CRISNER: A Practically Efficient Reasoner for Qualitative Preferences

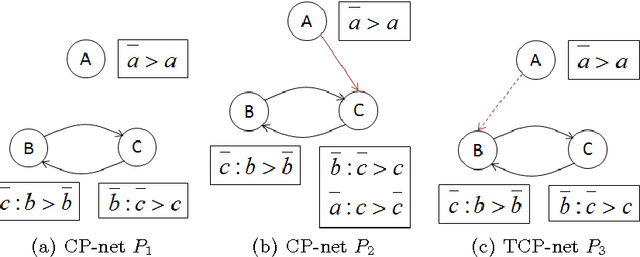
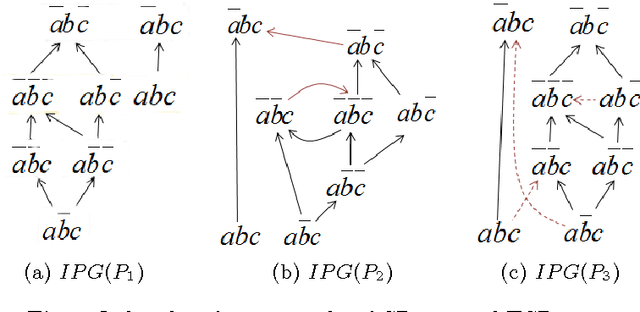
We present CRISNER (Conditional & Relative Importance Statement Network PrEference Reasoner), a tool that provides practically efficient as well as exact reasoning about qualitative preferences in popular ceteris paribus preference languages such as CP-nets, TCP-nets, CP-theories, etc. The tool uses a model checking engine to translate preference specifications and queries into appropriate Kripke models and verifiable properties over them respectively. The distinguishing features of the tool are: (1) exact and provably correct query answering for testing dominance, consistency with respect to a preference specification, and testing equivalence and subsumption of two sets of preferences; (2) automatic generation of proofs evidencing the correctness of answer produced by CRISNER to any of the above queries; (3) XML inputs and outputs that make it portable and pluggable into other applications. We also describe the extensible architecture of CRISNER, which can be extended to new reference formalisms based on ceteris paribus semantics that may be developed in the future.

Representing and Reasoning with Qualitative Preferences for Compositional Systems

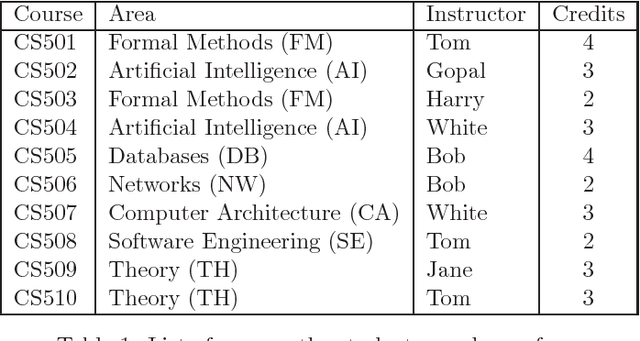
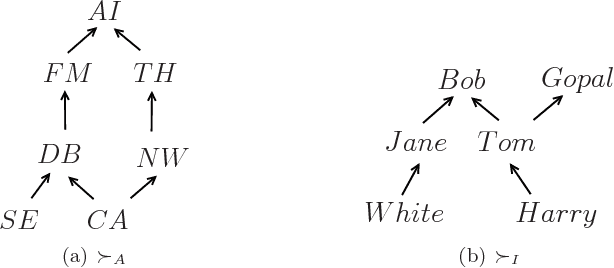
Many applications, e.g., Web service composition, complex system design, team formation, etc., rely on methods for identifying collections of objects or entities satisfying some functional requirement. Among the collections that satisfy the functional requirement, it is often necessary to identify one or more collections that are optimal with respect to user preferences over a set of attributes that describe the non-functional properties of the collection. We develop a formalism that lets users express the relative importance among attributes and qualitative preferences over the valuations of each attribute. We define a dominance relation that allows us to compare collections of objects in terms of preferences over attributes of the objects that make up the collection. We establish some key properties of the dominance relation. In particular, we show that the dominance relation is a strict partial order when the intra-attribute preference relations are strict partial orders and the relative importance preference relation is an interval order. We provide algorithms that use this dominance relation to identify the set of most preferred collections. We show that under certain conditions, the algorithms are guaranteed to return only (sound), all (complete), or at least one (weakly complete) of the most preferred collections. We present results of simulation experiments comparing the proposed algorithms with respect to (a) the quality of solutions (number of most preferred solutions) produced by the algorithms, and (b) their performance and efficiency. We also explore some interesting conjectures suggested by the results of our experiments that relate the properties of the user preferences, the dominance relation, and the algorithms.