Computing Evolutionarily Stable Strategies in Imperfect-Information Games

We present an algorithm for computing evolutionarily stable strategies (ESSs) in symmetric perfect-recall extensive-form games of imperfect information. Our main algorithm is for two-player games, and we describe how it can be extended to multiplayer games. The algorithm is sound and computes all ESSs in nondegenerate games and a subset of them in degenerate games which contain an infinite continuum of symmetric Nash equilibria. The algorithm is anytime and can be stopped early to find one or more ESSs. We experiment on an imperfect-information cancer signaling game as well as random games to demonstrate scalability.

Consistent Opponent Modeling of Static Opponents in Imperfect-Information Games

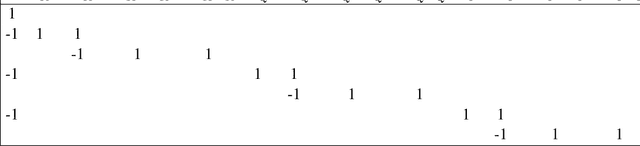
The goal of agents in multi-agent environments is to maximize total reward against the opposing agents that are encountered. Following a game-theoretic solution concept, such as Nash equilibrium, may obtain a strong performance in some settings; however, such approaches fail to capitalize on historical and observed data from repeated interactions against our opponents. Opponent modeling algorithms integrate machine learning techniques to exploit suboptimal opponents utilizing available data; however, the effectiveness of such approaches in imperfect-information games to date is quite limited. We show that existing opponent modeling approaches fail to satisfy a simple desirable property even against static opponents drawn from a known prior distribution; namely, they do not guarantee that the model approaches the opponent's true strategy even in the limit as the number of game iterations approaches infinity. We develop a new algorithm that is able to achieve this property and runs efficiently by solving a convex minimization problem based on the sequence-form game representation using projected gradient descent. The algorithm is guaranteed to efficiently converge to the opponent's true strategy given observations from gameplay and possibly additional historical data if it is available.

Dominated Actions in Imperfect-Information Games

Dominance is a fundamental concept in game theory. In strategic-form games dominated strategies can be identified in polynomial time. As a consequence, iterative removal of dominated strategies can be performed efficiently as a preprocessing step for reducing the size of a game before computing a Nash equilibrium. For imperfect-information games in extensive form, we could convert the game to strategic form and then iteratively remove dominated strategies in the same way; however, this conversion may cause an exponential blowup in game size. In this paper we define and study the concept of dominated actions in imperfect-information games. Our main result is a polynomial-time algorithm for determining whether an action is dominated (strictly or weakly) by any mixed strategy in n-player games, which can be extended to an algorithm for iteratively removing dominated actions. This allows us to efficiently reduce the size of the game tree as a preprocessing step for Nash equilibrium computation. We explore the role of dominated actions empirically in the "All In or Fold" No-Limit Texas Hold'em poker variant.

Nonparametric Strategy Test

We present a nonparametric statistical test for determining whether an agent is following a given mixed strategy in a repeated strategic-form game given samples of the agent's play. This involves two components: determining whether the agent's frequencies of pure strategies are sufficiently close to the target frequencies, and determining whether the pure strategies selected are independent between different game iterations. Our integrated test involves applying a chi-squared goodness of fit test for the first component and a generalized Wald-Wolfowitz runs test for the second component. The results from both tests are combined using Bonferroni correction to produce a complete test for a given significance level $\alpha.$ We applied the test to publicly available data of human rock-paper-scissors play. The data consists of 50 iterations of play for 500 human players. We test with a null hypothesis that the players are following a uniform random strategy independently at each game iteration. Using a significance level of $\alpha = 0.05$, we conclude that 305 (61%) of the subjects are following the target strategy.

Bayesian Opponent Modeling in Multiplayer Imperfect-Information Games

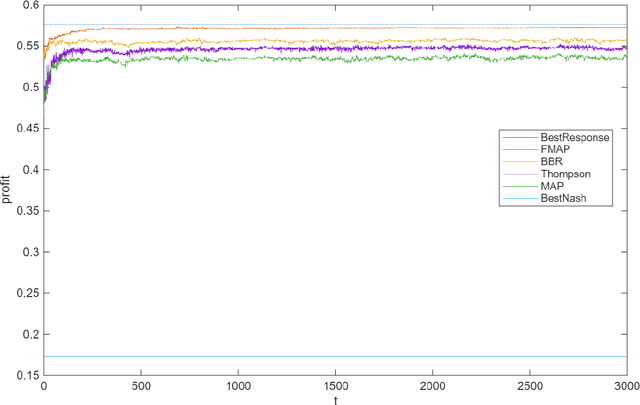
In many real-world settings agents engage in strategic interactions with multiple opposing agents who can employ a wide variety of strategies. The standard approach for designing agents for such settings is to compute or approximate a relevant game-theoretic solution concept such as Nash equilibrium and then follow the prescribed strategy. However, such a strategy ignores any observations of opponents' play, which may indicate shortcomings that can be exploited. We present an approach for opponent modeling in multiplayer imperfect-information games where we collect observations of opponents' play through repeated interactions. We run experiments against a wide variety of real opponents and exact Nash equilibrium strategies in three-player Kuhn poker and show that our algorithm significantly outperforms all of the agents, including the exact Nash equilibrium strategies.

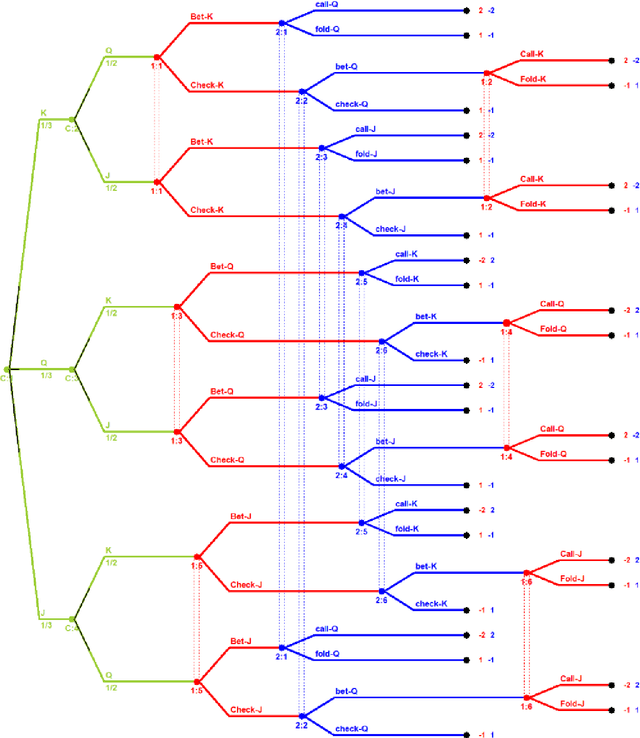
Observable Perfect Equilibrium

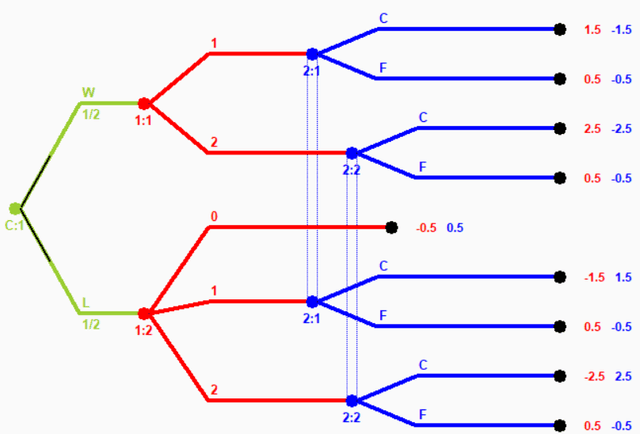
While Nash equilibrium has emerged as the central game-theoretic solution concept, many important games contain several Nash equilibria and we must determine how to select between them in order to create real strategic agents. Several Nash equilibrium refinement concepts have been proposed and studied for sequential imperfect-information games, the most prominent being trembling-hand perfect equilibrium, quasi-perfect equilibrium, and recently one-sided quasi-perfect equilibrium. These concepts are robust to certain arbitrarily small mistakes, and are guaranteed to always exist; however, we argue that neither of these is the correct concept for developing strong agents in sequential games of imperfect information. We define a new equilibrium refinement concept for extensive-form games called observable perfect equilibrium in which the solution is robust over trembles in publicly-observable action probabilities (not necessarily over all action probabilities that may not be observable by opposing players). Observable perfect equilibrium correctly captures the assumption that the opponent is playing as rationally as possible given mistakes that have been observed (while previous solution concepts do not). We prove that observable perfect equilibrium is always guaranteed to exist, and demonstrate that it leads to a different solution than the prior extensive-form refinements in no-limit poker. We expect observable perfect equilibrium to be a useful equilibrium refinement concept for modeling many important imperfect-information games of interest in artificial intelligence.

Fictitious Play with Maximin Initialization

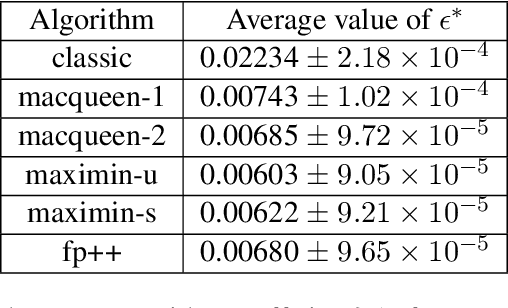
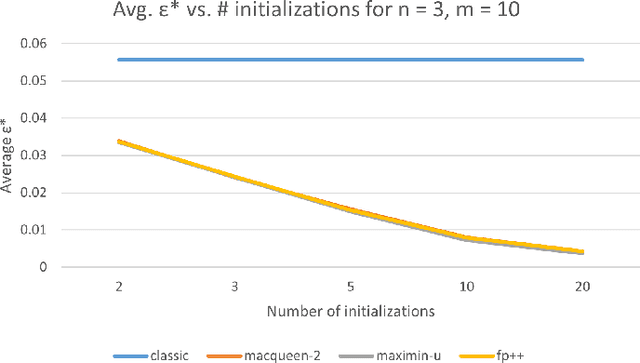
Fictitious play has recently emerged as the most accurate scalable algorithm for approximating Nash equilibrium strategies in multiplayer games. We show that the degree of equilibrium approximation error of fictitious play can be significantly reduced by carefully selecting the initial strategies. We present several new procedures for strategy initialization and compare them to the classic approach, which initializes all pure strategies to have equal probability. The best-performing approach, called maximin, solves a nonconvex quadratic program to compute initial strategies and results in a nearly 75% reduction in approximation error compared to the classic approach when 5 initializations are used.

Safe Equilibrium

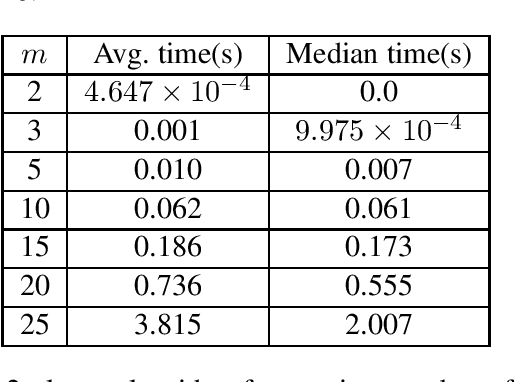
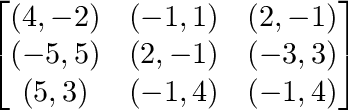
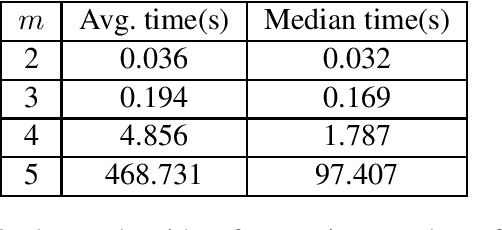
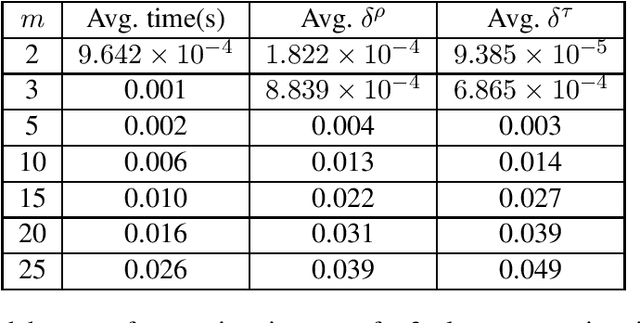
The standard game-theoretic solution concept, Nash equilibrium, assumes that all players behave rationally. If we follow a Nash equilibrium and opponents are irrational (or follow strategies from a different Nash equilibrium), then we may obtain an extremely low payoff. On the other hand, a maximin strategy assumes that all opposing agents are playing to minimize our payoff (even if it is not in their best interest), and ensures the maximal possible worst-case payoff, but results in exceedingly conservative play. We propose a new solution concept called safe equilibrium that models opponents as behaving rationally with a specified probability and behaving potentially arbitrarily with the remaining probability. We prove that a safe equilibrium exists in all strategic-form games (for all possible values of the rationality parameters), and prove that its computation is PPAD-hard. We present exact algorithms for computing a safe equilibrium in both 2 and $n$-player games, as well as scalable approximation algorithms.

Human strategic decision making in parametrized games

Many real-world games contain parameters which can affect payoffs, action spaces, and information states. For fixed values of the parameters, the game can be solved using standard algorithms. However, in many settings agents must act without knowing the values of the parameters that will be encountered in advance. Often the decisions must be made by a human under time and resource constraints, and it is unrealistic to assume that a human can solve the game in real time. We present a new framework that enables human decision makers to make fast decisions without the aid of real-time solvers. We demonstrate applicability to a variety of situations including settings with multiple players and imperfect information.

Computing Nash Equilibria in Multiplayer DAG-Structured Stochastic Games with Persistent Imperfect Information

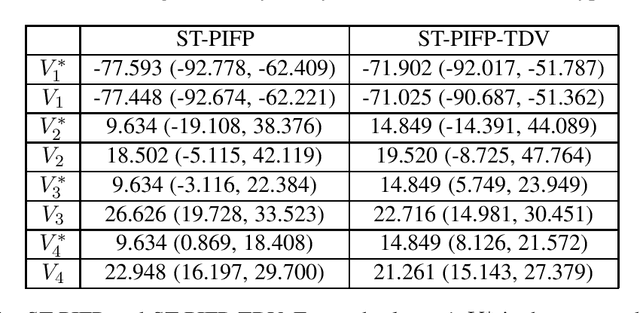
Many important real-world settings contain multiple players interacting over an unknown duration with probabilistic state transitions, and are naturally modeled as stochastic games. Prior research on algorithms for stochastic games has focused on two-player zero-sum games, games with perfect information, and games with imperfect-information that is local and does not extend between game states. We present an algorithm for approximating Nash equilibrium in multiplayer general-sum stochastic games with persistent imperfect information that extends throughout game play. We experiment on a 4-player imperfect-information naval strategic planning scenario. Using a new procedure, we are able to demonstrate that our algorithm computes a strategy that closely approximates Nash equilibrium in this game.