Riemannian Stochastic Gradient Method for Nested Composition Optimization

This work considers optimization of composition of functions in a nested form over Riemannian manifolds where each function contains an expectation. This type of problems is gaining popularity in applications such as policy evaluation in reinforcement learning or model customization in meta-learning. The standard Riemannian stochastic gradient methods for non-compositional optimization cannot be directly applied as stochastic approximation of inner functions create bias in the gradients of the outer functions. For two-level composition optimization, we present a Riemannian Stochastic Composition Gradient Descent (R-SCGD) method that finds an approximate stationary point, with expected squared Riemannian gradient smaller than $\epsilon$, in $O(\epsilon^{-2})$ calls to the stochastic gradient oracle of the outer function and stochastic function and gradient oracles of the inner function. Furthermore, we generalize the R-SCGD algorithms for problems with multi-level nested compositional structures, with the same complexity of $O(\epsilon^{-2})$ for the first-order stochastic oracle. Finally, the performance of the R-SCGD method is numerically evaluated over a policy evaluation problem in reinforcement learning.

Generalized Sparse Precision Matrix Selection for Fitting Multivariate Gaussian Random Fields to Large Data Sets

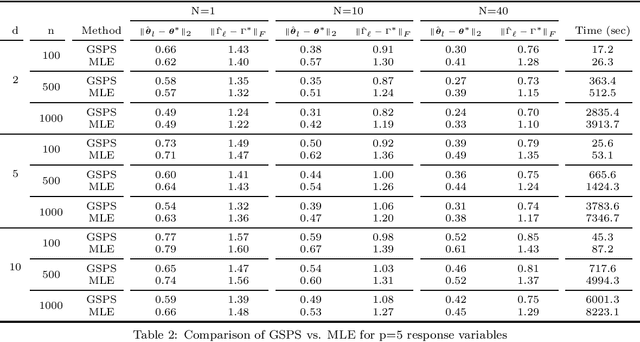
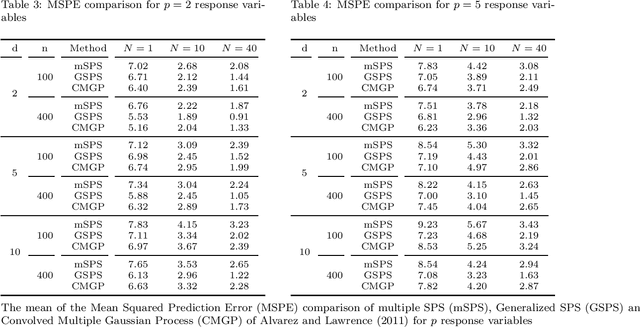
We present a new method for estimating multivariate, second-order stationary Gaussian Random Field (GRF) models based on the Sparse Precision matrix Selection (SPS) algorithm, proposed by Davanloo et al. (2015) for estimating scalar GRF models. Theoretical convergence rates for the estimated between-response covariance matrix and for the estimated parameters of the underlying spatial correlation function are established. Numerical tests using simulated and real datasets validate our theoretical findings. Data segmentation is used to handle large data sets.

Sparse Precision Matrix Selection for Fitting Gaussian Random Field Models to Large Data Sets

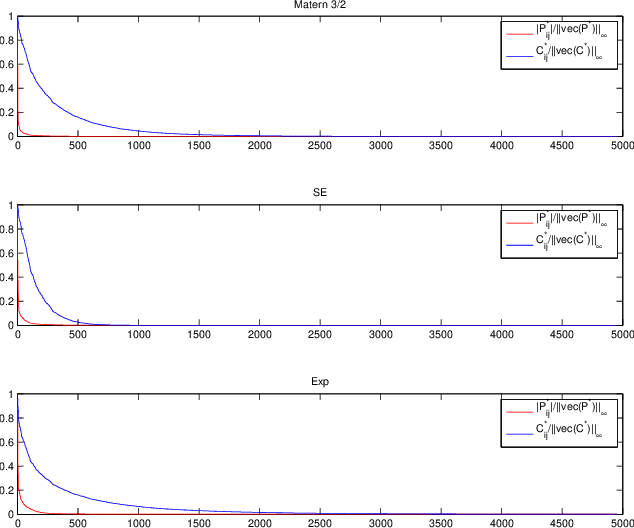
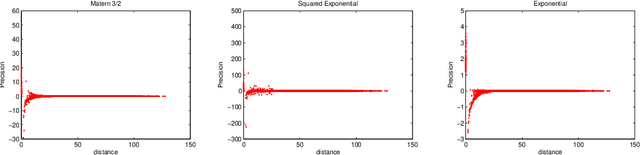
Iterative methods for fitting a Gaussian Random Field (GRF) model to spatial data via maximum likelihood (ML) require $\mathcal{O}(n^3)$ floating point operations per iteration, where $n$ denotes the number of data locations. For large data sets, the $\mathcal{O}(n^3)$ complexity per iteration together with the non-convexity of the ML problem render traditional ML methods inefficient for GRF fitting. The problem is even more aggravated for anisotropic GRFs where the number of covariance function parameters increases with the process domain dimension. In this paper, we propose a new two-step GRF estimation procedure when the process is second-order stationary. First, a \emph{convex} likelihood problem regularized with a weighted $\ell_1$-norm, utilizing the available distance information between observation locations, is solved to fit a sparse \emph{{precision} (inverse covariance) matrix to the observed data using the Alternating Direction Method of Multipliers. Second, the parameters of the GRF spatial covariance function are estimated by solving a least squares problem. Theoretical error bounds for the proposed estimator are provided; moreover, convergence of the estimator is shown as the number of samples per location increases. The proposed method is numerically compared with state-of-the-art methods for big $n$. Data segmentation schemes are implemented to handle large data sets.