VIPaint: Image Inpainting with Pre-Trained Diffusion Models via Variational Inference

Diffusion probabilistic models learn to remove noise that is artificially added to the data during training. Novel data, like images, may then be generated from Gaussian noise through a sequence of denoising operations. While this Markov process implicitly defines a joint distribution over noise-free data, it is not simple to condition the generative process on masked or partial images. A number of heuristic sampling procedures have been proposed for solving inverse problems with diffusion priors, but these approaches do not directly approximate the true conditional distribution imposed by inference queries, and are often ineffective for large masked regions. Moreover, many of these baselines cannot be applied to latent diffusion models which use image encodings for efficiency. We instead develop a hierarchical variational inference algorithm that analytically marginalizes missing features, and uses a rigorous variational bound to optimize a non-Gaussian Markov approximation of the true diffusion posterior. Through extensive experiments with both pixel-based and latent diffusion models of images, we show that our VIPaint method significantly outperforms previous approaches in both the plausibility and diversity of imputations, and is easily generalized to other inverse problems like deblurring and superresolution.

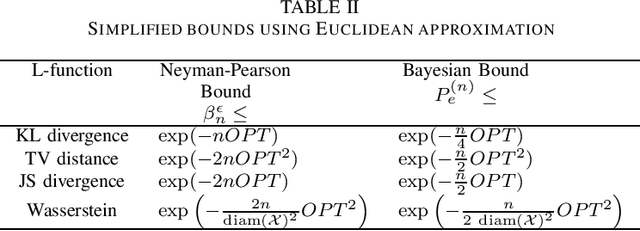
Limits of Deepfake Detection: A Robust Estimation Viewpoint

Deepfake detection is formulated as a hypothesis testing problem to classify an image as genuine or GAN-generated. A robust statistics view of GANs is considered to bound the error probability for various GAN implementations in terms of their performance. The bounds are further simplified using a Euclidean approximation for the low error regime. Lastly, relationships between error probability and epidemic thresholds for spreading processes in networks are established.