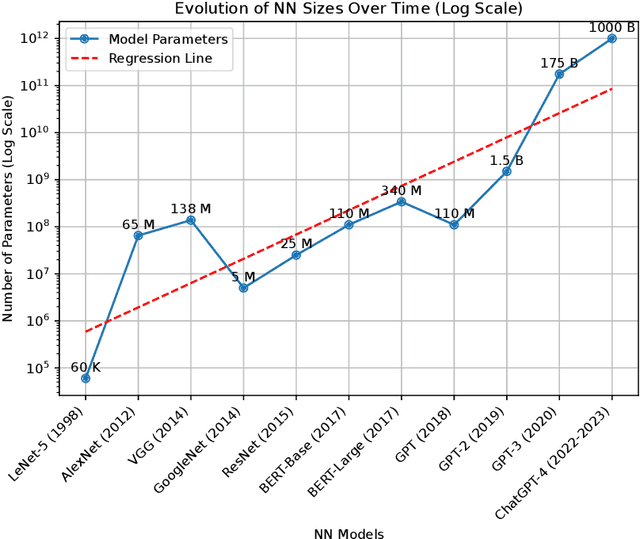
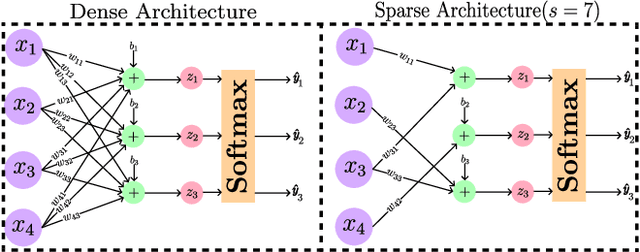
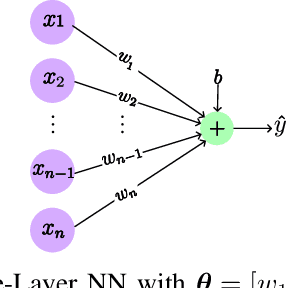
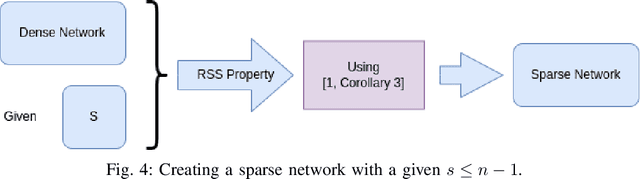
Learning a Sparse Neural Network using IHT

The core of a good model is in its ability to focus only on important information that reflects the basic patterns and consistencies, thus pulling out a clear, noise-free signal from the dataset. This necessitates using a simplified model defined by fewer parameters. The importance of theoretical foundations becomes clear in this context, as this paper relies on established results from the domain of advanced sparse optimization, particularly those addressing nonlinear differentiable functions. The need for such theoretical foundations is further highlighted by the trend that as computational power for training NNs increases, so does the complexity of the models in terms of a higher number of parameters. In practical scenarios, these large models are often simplified to more manageable versions with fewer parameters. Understanding why these simplified models with less number of parameters remain effective raises a crucial question. Understanding why these simplified models with fewer parameters remain effective raises an important question. This leads to the broader question of whether there is a theoretical framework that can clearly explain these empirical observations. Recent developments, such as establishing necessary conditions for the convergence of iterative hard thresholding (IHT) to a sparse local minimum (a sparse method analogous to gradient descent) are promising. The remarkable capacity of the IHT algorithm to accurately identify and learn the locations of nonzero parameters underscores its practical effectiveness and utility. This paper aims to investigate whether the theoretical prerequisites for such convergence are applicable in the realm of neural network (NN) training by providing justification for all the necessary conditions for convergence. Then, these conditions are validated by experiments on a single-layer NN, using the IRIS dataset as a testbed.

The Backpropagation algorithm for a math student

A Deep Neural Network (DNN) is a composite function of vector-valued functions, and in order to train a DNN, it is necessary to calculate the gradient of the loss function with respect to all parameters. This calculation can be a non-trivial task because the loss function of a DNN is a composition of several nonlinear functions, each with numerous parameters. The Backpropagation (BP) algorithm leverages the composite structure of the DNN to efficiently compute the gradient. As a result, the number of layers in the network does not significantly impact the complexity of the calculation. The objective of this paper is to express the gradient of the loss function in terms of a matrix multiplication using the Jacobian operator. This can be achieved by considering the total derivative of each layer with respect to its parameters and expressing it as a Jacobian matrix. The gradient can then be represented as the matrix product of these Jacobian matrices. This approach is valid because the chain rule can be applied to a composition of vector-valued functions, and the use of Jacobian matrices allows for the incorporation of multiple inputs and outputs. By providing concise mathematical justifications, the results can be made understandable and useful to a broad audience from various disciplines.

Convergence of the mini-batch SIHT algorithm

The Iterative Hard Thresholding (IHT) algorithm has been considered extensively as an effective deterministic algorithm for solving sparse optimizations. The IHT algorithm benefits from the information of the batch (full) gradient at each point and this information is a crucial key for the convergence analysis of the generated sequence. However, this strength becomes a weakness when it comes to machine learning and high dimensional statistical applications because calculating the batch gradient at each iteration is computationally expensive or impractical. Fortunately, in these applications the objective function has a summation structure that can be taken advantage of to approximate the batch gradient by the stochastic mini-batch gradient. In this paper, we study the mini-batch Stochastic IHT (SIHT) algorithm for solving the sparse optimizations. As opposed to previous works where increasing and variable mini-batch size is necessary for derivation, we fix the mini-batch size according to a lower bound that we derive and show our work. To prove stochastic convergence of the objective value function we first establish a critical sparse stochastic gradient descent property. Using this stochastic gradient descent property we show that the sequence generated by the stochastic mini-batch SIHT is a supermartingale sequence and converges with probability one. Unlike previous work we do not assume the function to be a restricted strongly convex. To the best of our knowledge, in the regime of sparse optimization, this is the first time in the literature that it is shown that the sequence of the stochastic function values converges with probability one by fixing the mini-batch size for all steps.

Amenable Sparse Network Investigator

As the optimization problem of pruning a neural network is nonconvex and the strategies are only guaranteed to find local solutions, a good initialization becomes paramount. To this end, we present the Amenable Sparse Network Investigator ASNI algorithm that learns a sparse network whose initialization is compressed. The learned sparse structure found by ASNI is amenable since its corresponding initialization, which is also learned by ASNI, consists of only 2L numbers, where L is the number of layers. Requiring just a few numbers for parameter initialization of the learned sparse network makes the sparse network amenable. The learned initialization set consists of L signed pairs that act as the centroids of parameter values of each layer. These centroids are learned by the ASNI algorithm after only one single round of training. We experimentally show that the learned centroids are sufficient to initialize the nonzero parameters of the learned sparse structure in order to achieve approximately the accuracy of non-sparse network. We also empirically show that in order to learn the centroids, one needs to prune the network globally and gradually. Hence, for parameter pruning we propose a novel strategy based on a sigmoid function that specifies the sparsity percentage across the network globally. Then, pruning is done magnitude-wise and after each epoch of training. We have performed a series of experiments utilizing networks such as ResNets, VGG-style, small convolutional, and fully connected ones on ImageNet, CIFAR10, and MNIST datasets.

On the Compression of Natural Language Models

Deep neural networks are effective feature extractors but they are prohibitively large for deployment scenarios. Due to the huge number of parameters, interpretability of parameters in different layers is not straight-forward. This is why neural networks are sometimes considered black boxes. Although simpler models are easier to explain, finding them is not easy. If found, a sparse network that can fit to a data from scratch would help to interpret parameters of a neural network. To this end, lottery ticket hypothesis states that typical dense neural networks contain a small sparse sub-network that can be trained to a reach similar test accuracy in an equal number of steps. The goal of this work is to assess whether such a trainable subnetwork exists for natural language models (NLM)s. To achieve this goal we will review state-of-the-art compression techniques such as quantization, knowledge distillation, and pruning.