Jinglai Shen
Learning a Sparse Neural Network using IHT
Apr 29, 2024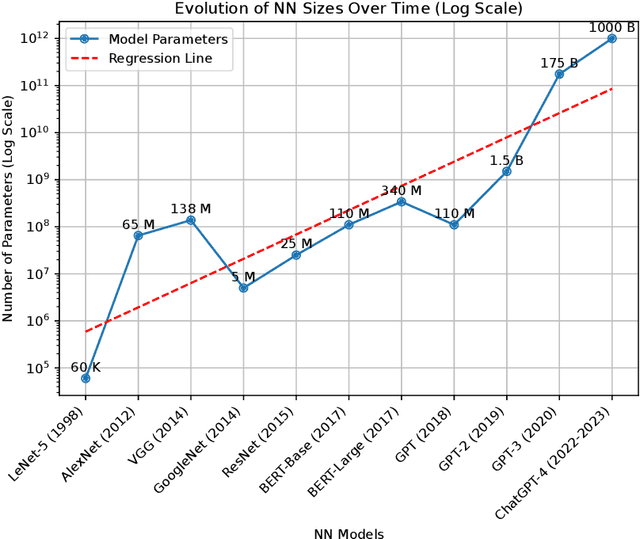
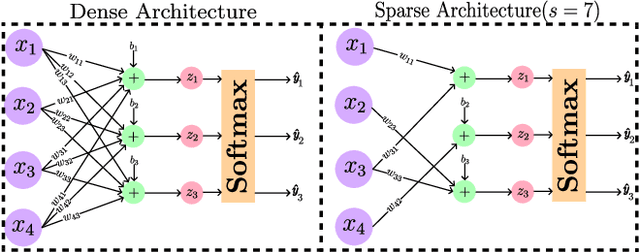
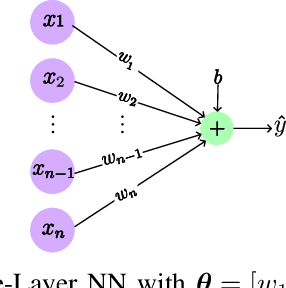
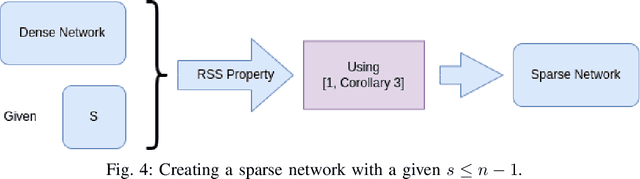
Abstract:The core of a good model is in its ability to focus only on important information that reflects the basic patterns and consistencies, thus pulling out a clear, noise-free signal from the dataset. This necessitates using a simplified model defined by fewer parameters. The importance of theoretical foundations becomes clear in this context, as this paper relies on established results from the domain of advanced sparse optimization, particularly those addressing nonlinear differentiable functions. The need for such theoretical foundations is further highlighted by the trend that as computational power for training NNs increases, so does the complexity of the models in terms of a higher number of parameters. In practical scenarios, these large models are often simplified to more manageable versions with fewer parameters. Understanding why these simplified models with less number of parameters remain effective raises a crucial question. Understanding why these simplified models with fewer parameters remain effective raises an important question. This leads to the broader question of whether there is a theoretical framework that can clearly explain these empirical observations. Recent developments, such as establishing necessary conditions for the convergence of iterative hard thresholding (IHT) to a sparse local minimum (a sparse method analogous to gradient descent) are promising. The remarkable capacity of the IHT algorithm to accurately identify and learn the locations of nonzero parameters underscores its practical effectiveness and utility. This paper aims to investigate whether the theoretical prerequisites for such convergence are applicable in the realm of neural network (NN) training by providing justification for all the necessary conditions for convergence. Then, these conditions are validated by experiments on a single-layer NN, using the IRIS dataset as a testbed.
Convergence of the mini-batch SIHT algorithm
Sep 29, 2022Abstract:The Iterative Hard Thresholding (IHT) algorithm has been considered extensively as an effective deterministic algorithm for solving sparse optimizations. The IHT algorithm benefits from the information of the batch (full) gradient at each point and this information is a crucial key for the convergence analysis of the generated sequence. However, this strength becomes a weakness when it comes to machine learning and high dimensional statistical applications because calculating the batch gradient at each iteration is computationally expensive or impractical. Fortunately, in these applications the objective function has a summation structure that can be taken advantage of to approximate the batch gradient by the stochastic mini-batch gradient. In this paper, we study the mini-batch Stochastic IHT (SIHT) algorithm for solving the sparse optimizations. As opposed to previous works where increasing and variable mini-batch size is necessary for derivation, we fix the mini-batch size according to a lower bound that we derive and show our work. To prove stochastic convergence of the objective value function we first establish a critical sparse stochastic gradient descent property. Using this stochastic gradient descent property we show that the sequence generated by the stochastic mini-batch SIHT is a supermartingale sequence and converges with probability one. Unlike previous work we do not assume the function to be a restricted strongly convex. To the best of our knowledge, in the regime of sparse optimization, this is the first time in the literature that it is shown that the sequence of the stochastic function values converges with probability one by fixing the mini-batch size for all steps.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge